题目内容
设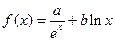 .
.
(1)若曲线 在点
在点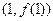 处的切线方程为
处的切线方程为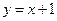 ,求
,求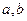 的值;
的值;
(2)当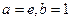 时,求
时,求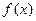 的单调区间与极值.
的单调区间与极值.
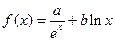 .
.(1)若曲线
 在点
在点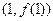 处的切线方程为
处的切线方程为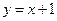 ,求
,求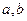 的值;
的值;(2)当
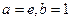 时,求
时,求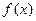 的单调区间与极值.
的单调区间与极值.(1)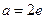 ,
,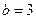
(2)单调增区间是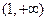 ,减区间是
,减区间是 ,极小值
,极小值
求导可得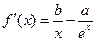 .
.
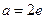 ,
,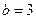
(2)单调增区间是
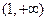 ,减区间是
,减区间是 ,极小值
,极小值
求导可得
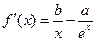 .
.(1)由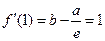 ,
,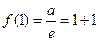 ,解得
,解得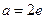 ,
,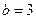 .
.
(2)函数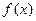 的定义域是
的定义域是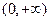 .
.
当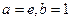 时,
时,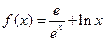 ,
,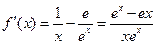 .
.
令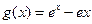 ,求导可得
,求导可得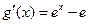 .
.
当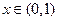 时,
时, ,则
,则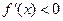 ,
,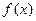 是减函数;
是减函数;
当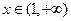 时,
时,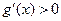 ,则
,则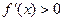 ,
,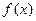 是增函数.
是增函数.
故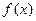 的单调增区间是
的单调增区间是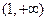 ,减区间是
,减区间是 ,当
,当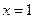 时,
时,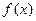 有极小值
有极小值 .
.
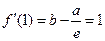 ,
,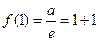 ,解得
,解得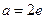 ,
,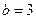 .
.(2)函数
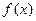 的定义域是
的定义域是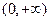 .
.当
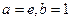 时,
时,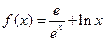 ,
,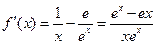 .
.令
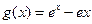 ,求导可得
,求导可得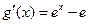 .
.当
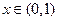 时,
时, ,则
,则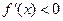 ,
,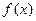 是减函数;
是减函数;当
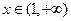 时,
时,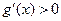 ,则
,则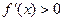 ,
,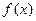 是增函数.
是增函数.故
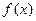 的单调增区间是
的单调增区间是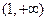 ,减区间是
,减区间是 ,当
,当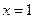 时,
时,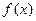 有极小值
有极小值 .
.
练习册系列答案
相关题目
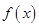 =
=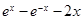 .
.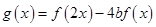 ,当
,当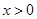 时,
时,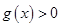 ,求
,求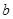 的最大值;
的最大值;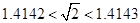 ,估计ln2的近似值(精确到0.001)
,估计ln2的近似值(精确到0.001)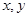 轴上滑动,点M在线段AB上,且
轴上滑动,点M在线段AB上,且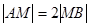 ,
,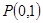 的直线
的直线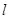 与曲线C交于不同两点E、F,N是曲线上不同于E、F的动点,求
与曲线C交于不同两点E、F,N是曲线上不同于E、F的动点,求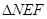 面积的最大值.
面积的最大值. .
. 在
在 时取得极值,求实数
时取得极值,求实数 的值;
的值; 对任意
对任意 恒成立,求实数
恒成立,求实数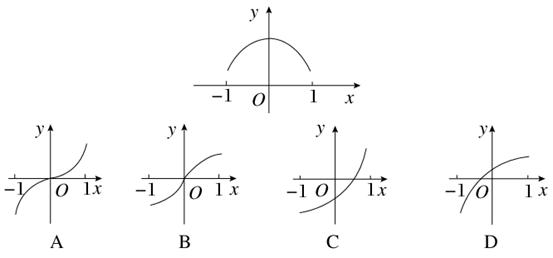
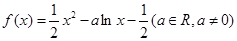 .
.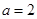 时,求曲线
时,求曲线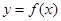 在点
在点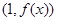 处的切线方程;
处的切线方程;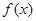 的单调区间;
的单调区间;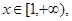 都有
都有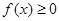 恒成立,求实数
恒成立,求实数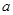 的取值范围.
的取值范围.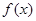 满足
满足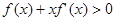 ,设
,设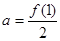 ,
,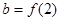 ,则
,则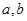 与
与 的大小关系为( )
的大小关系为( )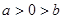
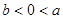
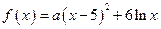 ,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).