题目内容
位于函数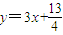
的图象上的一系列点P1（x1，y1），P2（x2，y2），…，Pn（xn，yn），…，这一系列点的横坐标构成以
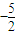为首项，-1为公差的等差数列{xn}．求点Pn的坐标；
【答案】分析：由Pn的横坐标构成以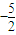
为首项，-1为公差的等差数列{xn}，求出数列{xn}的通项公式，并代入函数
的解析式，不难确定点Pn的坐标；
解答：解：由于Pn的横坐标构成以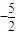
为首项，-1为公差的等差数列{xn}，
故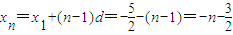
．
又Pn（xn，yn）位于函数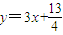
的图象上，
所以y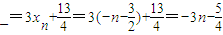
．
所求点Pn（xn，yn）的坐标为（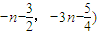
．
点评：本题考查的知识点是等差数列的通项公式，及直线的方程，由由Pn的横坐标构成等差数列{xn}，我们不难根据已知求出数列{xn}的通项公式，代入直线方程，求出对应的纵坐标，即可得到点的坐标．
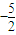为首项，-1为公差的等差数列{xn}，求出数列{xn}的通项公式，并代入函数的解析式，不难确定点Pn的坐标；解答：解：由于Pn的横坐标构成以
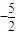为首项，-1为公差的等差数列{xn}，故
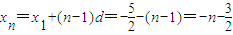．又Pn（xn，yn）位于函数
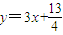的图象上，所以y
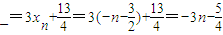．所求点Pn（xn，yn）的坐标为（
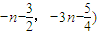．点评：本题考查的知识点是等差数列的通项公式，及直线的方程，由由Pn的横坐标构成等差数列{xn}，我们不难根据已知求出数列{xn}的通项公式，代入直线方程，求出对应的纵坐标，即可得到点的坐标．
练习册系列答案
相关题目
的图象上，且Pn的横坐标构成以
为首项，－1为公差的等差数列{xn}．
．
的图象上，且Pn的横坐标构成以
为首项，－1为公差的等差数列{xn}．
．
，
，等差数列{an}的任一项an∈S∩T，其中a1是S∩T中的最大数，－265＜a10＜－125，求{an}的通项公式．
的图象上，且Pn的横坐标构成以
为首项，－1为公差的等差数列{xn}．
．
的图象上的一系列点
,这一系列点的横坐标构成以
为首项,
为公差的等差数列
.
的坐标;
中的每一条的对称轴都垂直于
轴,对于
第
条抛物线
的顶点为
,且在该点处的切线的斜率为
,
.
的图象上的一系列点P1（x1，y1），P2（x2，y2），…，Pn（xn，yn），…，这一系列点的横坐标构成以-
为首项，-1为公差的等差数列{xn}。
。