题目内容
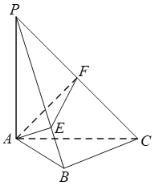
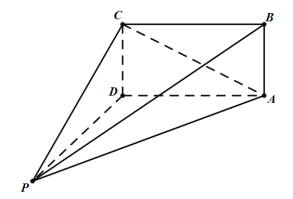
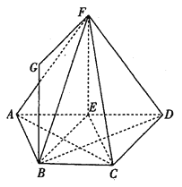
【题目】如图,已知![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,
且![]() 是
是![]() 的中点,
的中点,![]() .
.
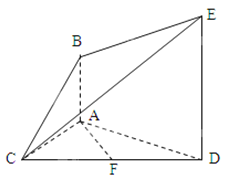
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求此多面体的体积.
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】
试题(1)取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,结合三角形中位线定理,可得
,结合三角形中位线定理,可得![]() ,且
,且![]() ,进而得到
,进而得到![]() ,结合线面平行的判定定理,即可得到
,结合线面平行的判定定理,即可得到![]() 平面
平面![]() ;(2)首先判断
;(2)首先判断![]() 为正三角形,结合
为正三角形,结合![]() 为中点可得
为中点可得![]() ,又由已知可得
,又由已知可得![]() ,根据线面垂直的判定定理,可得
,根据线面垂直的判定定理,可得![]() 平面
平面![]() ,进而根据面面平行的判定定理,得到平面
,进而根据面面平行的判定定理,得到平面![]() 平面
平面![]() ;(3)多面体是以
;(3)多面体是以![]() 为顶点,以四边形
为顶点,以四边形![]() 为底边的四棱锥,求出棱锥的高及底面面积,然后代入棱锥的体积公式,即可求出答案.
为底边的四棱锥,求出棱锥的高及底面面积,然后代入棱锥的体积公式,即可求出答案.
试题解析:(1)取![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() ,
,![]() 为
为![]() 的中点,
的中点, ,且
![]() ,又
,又![]() ,且
,且![]()
![]() ,且
,且![]() ,
,![]() 为平行四边形,
为平行四边形,![]() , 又
, 又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() ,所以
,所以![]() 为正三角形,
为正三角形,![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,![]() 平面
平面![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ;
;
(3)此多面体是一个以![]() 为定点,以四边形
为定点,以四边形![]() 为底边的四棱锥,
为底边的四棱锥,
![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 等边三角形
等边三角形![]() 边上的高就是四棱锥的高,
边上的高就是四棱锥的高,![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】共享单车的投放,方便了市民短途出行,被誉为中国“新四大发明”之一.某市为研究单车用户与年龄的相关程度,随机调查了100位成人市民,统计数据如下:
不小于40岁 | 小于40岁 | 合计 | |
单车用户 | 12 | 18 | 30 |
非单车用户 | 38 | 32 | 70 |
合计 | 50 | 50 | 100 |
(1)从独立性检验角度分析,能否有![]() 以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关;
以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关;
(2)将此样本的频率做为概率,从该市单车用户中随机抽取3人,记不小于40岁的单车用户的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
下面临界值表供参考:
P( | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: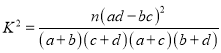 ,其中
,其中![]() )
)