题目内容
【题目】学校为了解学生在课外读物方面的支出情况,抽取了n名同学进行调查,结果显示这些同学的支出都在[10,50)(单位:元),其中支出在[30,50)(单位:元)的同学有67人,其频率分布直方图如图所示,则n的值为( )
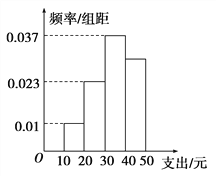
A. 100 B. 120 C. 130 D. 390
【答案】A
【解析】试题分析:根据小矩形的面积之和,算出位于10~30的2组数的频率之和为0.33,从而得到位于30~50的数据的频率之和为1﹣0.33=0.67,再由频率计算公式即可算出样本容量n的值.
解:∵位于10~20、20~30的小矩形的面积分别为
S1=0.01×10=0.1,S2=0.023×10=0.23,
∴位于10~20、20~30的据的频率分别为0.1、0.23
可得位于10~30的前3组数的频率之和为0.1+0.23=0.33
由此可得位于30~50数据的频率之和为1﹣0.33=0.67
∵支出在[30,50)的同学有67人,即位于30~50的频数为67,
∴根据频率计算公式,可得![]() =0.67,解之得n=100
=0.67,解之得n=100
故选:A

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
【题目】某成衣批发店为了对一款成衣进行合理定价,将该款成衣按事先拟定的价格进行试销,得到了如下数据:
批发单价x(元) | 80 | 82 | 84 | 86 | 88 | 90 |
销售量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程 ![]() ,其中
,其中 ![]()
(2)预测批发单价定为85元时,销售量大概是多少件?
(3)假设在今后的销售中,销售量与批发单价仍然服从(1)中的关系,且该款成衣的成本价为40元/件,为使该成衣批发店在该款成衣上获得更大利润,该款成衣单价大约定为多少元?