题目内容
7.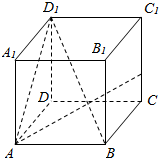 在棱长为4的正方体ABCD-A1B1C1D1中,点P在棱CC1上,且CC1=4CP.
在棱长为4的正方体ABCD-A1B1C1D1中,点P在棱CC1上,且CC1=4CP.(1)求直线AP与平面BCC1B1所成的角的正弦值大小;
(2)求点P到平面ABD1的距离.
分析 (1)由题设条件,连接PB,即可得出AP与平面BCC1B1所成的角为∠APB,用公式求出线面角的正弦.
(2)建立空间坐标系,用向量法求点到面的距离,求线段对应的向量在面的法向量的投影的长度即可.
解答  解:(1)如图,连接PB,由正方体的性质知∠APB即为所求的线面角,
解:(1)如图,连接PB,由正方体的性质知∠APB即为所求的线面角,
∵CC1=4CP,∴CP=1,由勾股定理知BP=$\sqrt{17}$,AB=$\sqrt{33}$
∴sin∠APB=$\frac{4}{\sqrt{33}}$=$\frac{4\sqrt{33}}{33}$;
(2)建立如图的空间坐标系,由已知D(0,0,0),A(4,0,0),C(0,4,0),D(0,0,4),B(4,4,0)
如图$\overrightarrow{AB}$=(0,4,0),$\overrightarrow{A{D}_{1}}$=(-4,0,4)$\overrightarrow{AP}$=(-4,4,1)
令面ABD1的法向量为$\overrightarrow{n}$=(x,y,z)
故有$\left\{\begin{array}{l}{x-z=0}\\{y=0}\end{array}\right.$
令x=1,则z=1,故$\overrightarrow{n}$=(1,0,1)
故点P到平面ABD1的距离d=$\frac{|-4+1|}{\sqrt{2}}$=$\frac{3}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$.
点评 本题考查线面角,考查向量法求点到面的距离,在做题时应根据题目的条件灵活选用解题的方法.

练习册系列答案
相关题目
15.已知向量$\vec a$与向量$\vec b$夹角为$\frac{π}{6}$,且$|\vec a|=\sqrt{3}$,$\vec a⊥(\vec a-2\vec b)$,则$|\vec b|$=( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 1 | D. | 2 |
12.三个数a=0.72,b=log20.7,c=20.7之间的大小关系是( )
| A. | a<c<b. | B. | a<b<c | C. | b<a<c | D. | b<c<a |
16.已知角α的终边经过点$(-1,\sqrt{3})$,则对函数f(x)=sinαcos2x+cosαcos(2x-$\frac{π}{2}$)的表述正确的是( )
| A. | 对称中心为($\frac{11}{12}π$,0) | |
| B. | 函数y=sin2x向左平移$\frac{π}{3}$个单位可得到f(x) | |
| C. | f(x)在区间$(-\frac{π}{3},\frac{π}{6})$上递增 | |
| D. | 方程f(x)=0在$[{-\frac{5}{6}π,0}]$上有三个零点 |



