题目内容
(本小题满分13分)
某零售店近五个月的销售额和利润额资料如下表:
| 商店名称 | A | B | C | D | E E |
销售额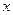 (千万元) (千万元) | 3 | 5 | 6 | 7 | 9 9 |
利润额 (百万元) (百万元) | 2 | 3 | 3 | 4 | 5 |
 相关关系;
相关关系;(2)用最小二乘法计算利润额
 关于销售额
关于销售额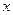 的回归直线方程;
的回归直线方程;(3)当销售额为4(千万元)时,利用(2)的结论估计该零售店的利润额(百万元).
(1)散点图如下. …………2分
两个变量呈正线性相关关系. …………4分
说明:①五个点中,全对的得2分,全错的得0分,不全对的得1分;
②答到正相关就给2分.

(2)设回归直线的方程是: .
.
由题中的数据可知 . …………6分
. …………6分
所以
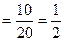 . …………8分
. …………8分 .
.
所以利润额 关于销售额
关于销售额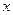 的回归直线方程为
的回归直线方程为 . …………10分
. …………10分
(3)由(2)知,当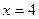 时,
时, =2.4, …………12分
=2.4, …………12分
所以当销售额为4(千万元)时,可以估计该店的利润额为2.4(百万元). ………13分
解析

(本小题满分14分)
为了调查老年人的身体状况,某老年活动中心对80位男性老年人和100位女性老年人在一次慢跑后的心率水平作了记录,记录结果如下列两个表格所示,
表1:80位男性老年人的心率水平的频数分布表(单位:次/分钟)
| 心率水平 |  | 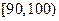 | 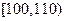 | 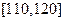 |
| 频数 | 10 | 40 | 20 | 10 |
| 心率水平 |  | 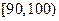 | 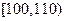 | 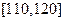 |
| 频数 | 10 | 20 | 50 | 20 |
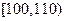 内的概率;
内的概率;(2)根据表2,完成下面的频率分布直方图,并由此估计这100女性老人心率水平的中位数;

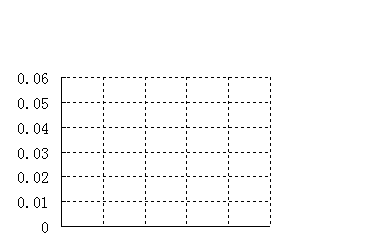
(3)完成下面2×2列联表,并回答能否在犯错误的概率不超过0.001的前提下认为“这180位老人的心率水平是否低于100与性别有关”.
表3:
| 心率水平 性别 | 心率小于100 | 心率大于或等于100 | 合计 |
| 男性 |  | 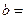 | |
| 女性 | 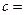 | 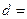 | |
| 合计 | | | 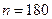 |
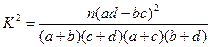
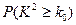 | 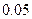 | 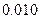 | 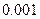 |
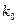 | 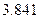 | 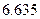 | 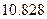 |
某研究机构为研究人的脚的大小与身高之间的关系,随机抽测了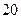 人,得到如下数据:
人,得到如下数据:
| 序号 | 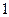 | 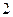 | 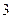 | 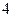 | 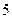 | 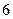 | 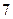 |  | 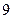 | 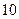 |
身高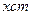 | 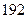 | 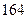 | 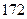 | 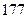 | 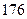 | 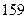 | 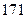 | 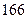 | 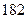 | 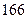 |
脚长 (码) (码) | 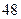 | 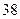 | 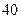 | 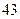 | 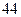 | 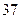 | 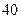 |  | 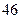 |  |
| 序号 | 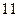 | 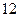 | 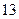 | 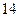 | 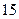 | 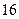 | 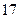 | 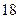 | 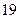 | 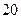 |
身高 | 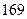 | 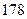 | 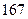 | 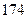 | 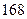 |  | 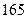 | 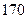 | 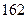 | 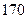 |
脚长 (码) (码) | 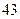 | 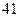 | 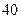 | 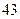 | 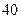 | 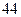 | 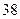 | 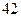 |  | 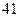 |
(1)若“身高大于
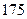 厘米”的为“高个”,“身高小于等于
厘米”的为“高个”,“身高小于等于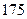 厘米”的为“非高个”;“脚长大于
厘米”的为“非高个”;“脚长大于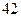 码”的为“大脚”,“脚长小于等于
码”的为“大脚”,“脚长小于等于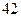 码”的为“非大脚”.
码”的为“非大脚”.请根据上表数据完成下面的
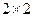 列联表:
列联表: | | 高 个 | 非高个 | 合 计 |
| 大 脚 | | | |
| 非大脚 | |  | |
| 合 计 | | |  |
(2)根据题(1)中表格的数据,检验人的脚的大小与身高之间是否有关系,若有关系指出判断有关系的把握性有多大?
某市为了保障民生,防止居民住房价格过快增长,计划出台合理的房价调控政策,为此有关部门抽样调查了100个楼盘的住房销售价格,右表是这100个楼盘住房销售均价(单位:千元/平米)的频率分布表,根据右表回答以下问题: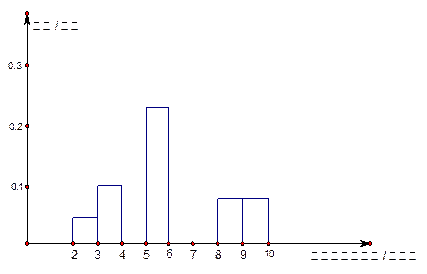
(1)求右表中a,b的值;
(2)请将下面的频率分布直方图补充完整,并根据直方图估计该市居民住房销售价格在4千元/平米
到8千元/平米之间的概率.
| 分组 | 频数 | 频率 |
| [2,3) | 5 | 0.05 |
| [3,4) | 10 | 0.10 |
| [4,5) | a | 0.15 |
| [5,6) | 24 | 0.24 |
| [6,7) | 18 | 0.18 |
| [7,8) | 12 | b |
| [8,9) | 8 | 0.08 |
| [9,10) | 8 | 0.08 |
| 合计 | 100 | 1.00 |
学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座,每科一节课,每节至少有一科,且数学、理综不安排在同一节,则不同的安排方法共有 ( )
| A.36种 | B.30种 | C.24种 | D.6种 |
 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为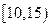 ,
, ,
, ,
, ,
,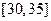 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在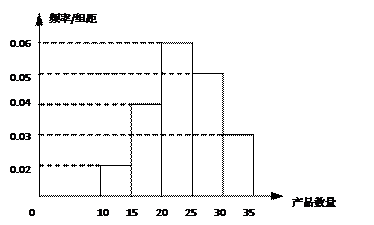
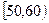 ,
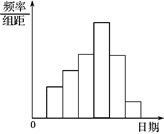
,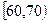 …
…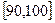 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题