题目内容

（本题满分14分）
某营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水
化合物，6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳
水化合物，6个单位的蛋白质和10个单位的维生素C.另外，该儿童这两餐需要的营状中
至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，
并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐？

设为该儿童分别预订个单位的午餐和个单位的晚餐，设费用为F，则F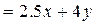，由题意知：





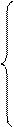
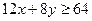
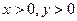
画出可行域：
…………………………………………………………10
变换目标函数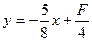：，当目标函数过点A，即直线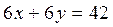和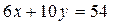的交点（4，3），F取得最小值，即要满足营养需要且花费最少，该儿童应当分别订4个单位的午餐和3个单位的晚餐。……………………….14

解析

练习册系列答案
相关题目

（本小题满分12分）为了了解学生身高情况，某校以10%的比例对全校700名学生按性别进行分层抽样调查，测得身高情况的统计图如下：

（1）估计该校男生的人数；
（2）估计该校学生身高在170~185cm之间的概率；
（3）从样本中身高在180~190cm之间的男生中任选2人，
求至少有1人身高在185~190cm之间的概率。

（本小题满分10分）
从甲、乙两名学生中选拔一人参加射箭比赛，为此需要对他们的射箭水平进行测试．现这两名学生在相同条件下各射箭7次，命中的环数如下：

甲
 		10
 		8
 		6
 		9
 		7
 		6
 		10
 
乙
 		10
 		9
 		8
 		6
 		7
 		8
 		8
 
（1）计算甲、乙两人射箭命中环数的平均数和方差；
（2）比较两个人的成绩，然后决定选择哪名学生参加射箭比赛．

（本小题满分13分）
某零售店近五个月的销售额和利润额资料如下表：

商店名称
A
B
C
D
E
E
销售额 (千万元)
3
5
6
7
9
9
利润额(百万元)
2
3
3
4
5
（1）画出散点图．观察散点图，说明两个变量有怎样的相关关系；
（2）用最小二乘法计算利润额关于销售额的回归直线方程；
（3）当销售额为4(千万元)时，利用（2）的结论估计该零售店的利润额（百万元）.

（本小题满分14分）
为积极响应国家“家电下乡”政策的号召，某厂家把总价值为10万元的A、B两种型号的电视机投放市场，并且全部被农民购买。若投放的A、B两种型号的电视机价值都不低于1万元，农民购买A、B两种型号的电视机将按电视机价值的一定比例给予补贴，补贴方案如下表所示，设投放市场的A、B型号电视机的价值分别为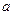万元,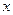万元，农民得到的补贴为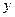万元,解答以下问题.

 
 		A型号
 		B型号
 
电视机价值(万元)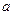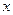
 
 
 
农民获得补贴(万元)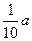
 
 
 
 
(1) 用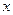的代数式表示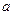
(2) 当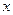取何值时, 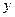取最大值并求出其最大值（精确到0.1，参考数据：）

若展开式中只有第六项的二项式系数最大，则展开式中的常数项是（   ）

A．B．C．D．

有一个容量为100的样本，数据的分组及各组的频数如下：

（1）列出样本的频率分布表；（2）画出频率分布直方图和频率折线图。

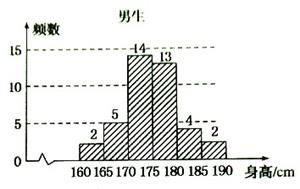
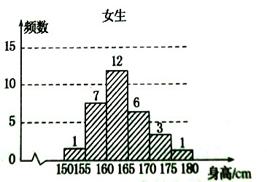
（本题满分14分）某研究小组为了研究学生的数学成绩与物理成绩之间的关系，随机抽取高二年级20名学生某次考试的成绩（百分制）如下表所示：

序号
1
  2
  3
  4
  5
 6
  7
  8
9
10
数学成绩
95
 75
 80
  94
  92
  65
 67
  84
 98
71
物理成绩
 90
 63
 72
  87
  91
  71
 58
  82
 93
80
序号
11
 12
 13
  14
  15
  16
  17
  18
19
20
数学成绩
67
 93
 64
  78
  77
  90
  57
  84
 72
83
物理成绩
 77
 82
 48
  85
  69
  91
  61
  82
 78
86
若数学成绩90分（含90分）以上为优秀，物理成绩85分（含85分）以上为优秀。
⑴根据上表完成下面的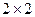列联表：
 
数学成绩优秀
数学成绩不优秀
合计
物理成绩优秀
 
      
  
物理成绩不优秀
 
       12
    
合计
 
      
    20
⑵根据⑴中表格的数据计算，有多少的把握，认为学生的数学成绩与物理成绩之间有关系？

（12分） 在对人们的休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人。女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动。
（1）根据以上数据建立一个2×2的列联表；
（2）判断性别与休闲方式是否有关系。
参考数据


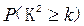0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001

0. 455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网