题目内容
(本小题共13分)
为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为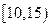 ,
, ,
, ,
, ,
,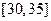 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工
人不在同一组的概率是多少?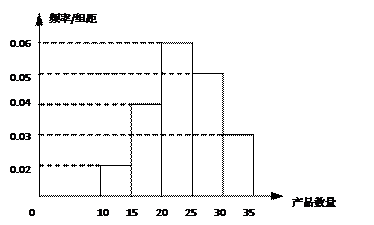
(Ⅰ)根据直方图可知产品件数在 内的人数为
内的人数为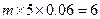 ,则
,则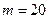 (位). ---------------- 6分
(位). ---------------- 6分
(Ⅱ)根据直方图可知产品件数在 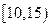 ,
, ,组内的人数分别为2,4.
,组内的人数分别为2,4.
设这2位工人不在同一组为A事件,则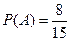 .
.
答:选取这2人不在同组的概率为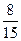 . ---------------- 13分
. ---------------- 13分
解析

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
(本题14分) 高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
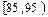 | ① | 0. 025 |
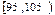 | | 0.050 |
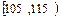 | | 0.200 |
 | 12 | 0.300 |
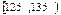 | | 0.275 |
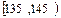 | 4 | ② |
| [145,155] | | 0.050 |
| 合计 | | ③ |
|
(1)根据上面图表,①②③处的数值分别为 ▲ 、 ▲ 、 ▲ ;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体落在[125,155]中的概率.
(本小题满分14分)
为积极响应国家“家电下乡”政策的号召,某厂家把总价值为10万元的A、B两种型号的电视机投放市场,并且全部被农民购买。若投放的A、B两种型号的电视机价值都不低于1万元,农民购买A、B两种型号的电视机将按电视机价值的一定比例给予补贴,补贴方案如下表所示,设投放市场的A、B型号电视机的价值分别为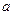 万元,
万元,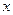 万元,农民得到的补贴为
万元,农民得到的补贴为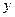 万元,解答以下问题.
万元,解答以下问题.
| | A型号 | B型号 |
| 电视机价值(万元) | 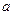 | 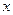 |
| 农民获得补贴(万元) | 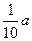 |  |
(1) 用
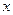 的代数式表示
的代数式表示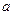
(2) 当
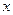 取何值时,
取何值时, 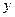 取最大值并求出其最大值(精确到0.1,参考数据:
取最大值并求出其最大值(精确到0.1,参考数据: )
) 在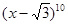 的展开式中,x6的系数是( )
的展开式中,x6的系数是( )
A.﹣27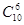 | B.27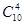 | C.﹣9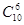 | D.9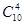 |
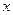 (千万元)
(千万元) (百万元)
(百万元) 相关关系;
相关关系;

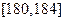
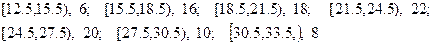
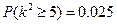 ,
,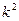 的观测值为
的观测值为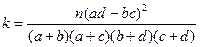 )
)