题目内容
已知函数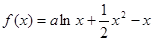
(Ⅰ)当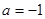 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)若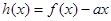 ,对定义域内任意x,均有
,对定义域内任意x,均有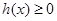 恒成立,求实数a的取值范围?
恒成立,求实数a的取值范围?
(Ⅲ)证明:对任意的正整数 ,
,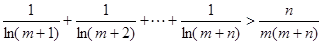 恒成立。
恒成立。
(Ⅰ) 在
在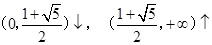 ;(Ⅱ)
;(Ⅱ)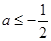 ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
解析试题分析:(Ⅰ)当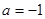 时,求函数
时,求函数 的单调区间,首先确定定义域
的单调区间,首先确定定义域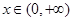 ,可通过单调性的定义,或求导确定单调区间,由于
,可通过单调性的定义,或求导确定单调区间,由于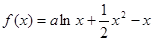 ,含有对数函数,可通过求导来确定单调区间,对函数
,含有对数函数,可通过求导来确定单调区间,对函数 求导得
求导得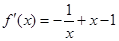 ,由此令
,由此令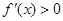 ,
, ,解出
,解出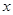 就能求出函数
就能求出函数 的单调区间;(Ⅱ)若
的单调区间;(Ⅱ)若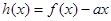 ,对定义域内任意
,对定义域内任意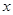 ,均有
,均有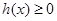 恒成立,求实数
恒成立,求实数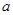 的取值范围,而
的取值范围,而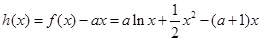 ,对定义域内任意
,对定义域内任意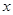 ,均有
,均有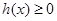 恒成立,属于恒成立问题,解这一类题,常常采用含有参数
恒成立,属于恒成立问题,解这一类题,常常采用含有参数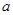 的放到不等式的一边,不含参数
的放到不等式的一边,不含参数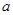 (即含
(即含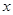 )的放到不等式的另一边,转化为函数的最值问题,但此题用此法比较麻烦,可考虑求其最小值,让最小值大于等于零即可,因此对函数
)的放到不等式的另一边,转化为函数的最值问题,但此题用此法比较麻烦,可考虑求其最小值,让最小值大于等于零即可,因此对函数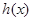 求导,利用导数确定最小值,从而求出
求导,利用导数确定最小值,从而求出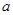 的取值范围;(Ⅲ)由(Ⅱ)知,当
的取值范围;(Ⅲ)由(Ⅱ)知,当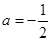 时,
时,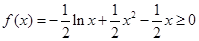 ,当且仅当
,当且仅当 时,等号成立,这个不等式等价于
时,等号成立,这个不等式等价于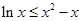 ,即
,即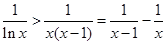 ,由此对任意的正整数
,由此对任意的正整数 ,不等式
,不等式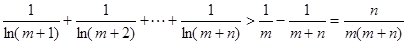 恒成立.
恒成立.
试题解析:(Ⅰ)定义域为(0,+∞),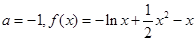 ,
,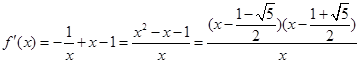 ,所以
,所以 在
在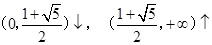 (4分)
(4分)
(Ⅱ)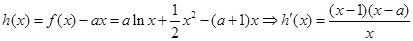 ,当
,当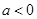 时,
时,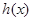 在
在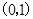 上递减,在
上递减,在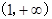 上递增,
上递增,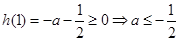 ,当
,当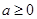 时,
时, 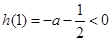 不可能成立,综上
不可能成立,综上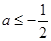 ;(9分)
;(9分)
(Ⅲ)令 ,
,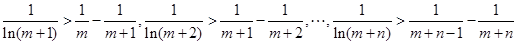 相加得到
相加得到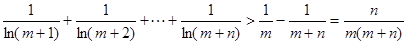
得证。(14分)
考点:函数与导数,函数的单调区间,函数与不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
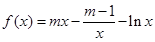 ,
, 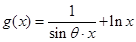 在
在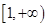 上为增函数,且
上为增函数,且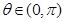 ,求解下列各题:
,求解下列各题: 的取值范围;
的取值范围; 在
在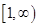 上为单调增函数,求
上为单调增函数,求 的取值范围;
的取值范围;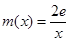 ,若在
,若在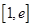 上至少存在一个
上至少存在一个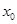 ,使得
,使得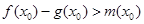 成立,求
成立,求 .
. ,
, 时,求函数
时,求函数 的最大值;
的最大值; ,其图象上存在一点
,其图象上存在一点 ,使此处切线的斜率
,使此处切线的斜率 ,求实数
,求实数 的取值范围;
的取值范围; ,
, ,
, 时,方程
时,方程 有唯一实数解,求
有唯一实数解,求 的值.
的值.
 在点
在点 处的切线与圆
处的切线与圆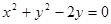 相切,求
相切,求 的值;
的值; 时,函数
时,函数 轴的上方,试求出
轴的上方,试求出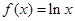 ,
,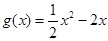 .
.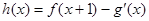 (其中
(其中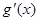 是
是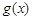 的导函数),求
的导函数),求 的最大值;
的最大值;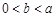 时,有
时,有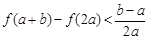 ;
;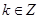 ,当
,当 时,不等式
时,不等式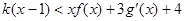 恒成立,求
恒成立,求 的最大值.
的最大值. 的一个焦点是
的一个焦点是 ,一条渐近线的方程是
,一条渐近线的方程是 .
. 为斜率的直线
为斜率的直线 与双曲线
与双曲线 ,且线段
,且线段 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为 ,求
,求 的取值范围.
的取值范围.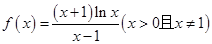 ,
, 的单调性;
的单调性;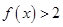 .
.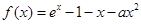 .
.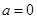 ,求
,求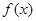 的单调区间;
的单调区间;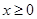 时
时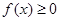 ,求
,求 的取值范围
的取值范围 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式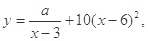 其中
其中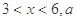 为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.己知销售价格为5元/千克时,每日可售出该商品11千克. 的值;
的值;