题目内容
设函数 .
.
(1)当 ,
, 时,求函数
时,求函数 的最大值;
的最大值;
(2)令 ,其图象上存在一点
,其图象上存在一点 ,使此处切线的斜率
,使此处切线的斜率 ,求实数
,求实数 的取值范围;
的取值范围;
(3)当 ,
, ,
, 时,方程
时,方程 有唯一实数解,求
有唯一实数解,求 的值.
的值.
(1)函数 的最大值为
的最大值为 ;(2)实数
;(2)实数 的取值范围是
的取值范围是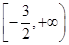 ;(3)
;(3)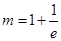 .
.
解析试题分析:(1)将 ,
,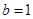 代入函数
代入函数 的解析式,然后利用导数求出函数
的解析式,然后利用导数求出函数 的最大值;(2)先确定函数
的最大值;(2)先确定函数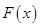 的解析式,并求出函数
的解析式,并求出函数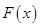 的导数,然后利用导数的几何意义将问题转化为
的导数,然后利用导数的几何意义将问题转化为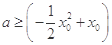 ,利用恒成立的思想进行求解;(3)将
,利用恒成立的思想进行求解;(3)将 ,
, 代入函数
代入函数 的解析式并确定函数
的解析式并确定函数 的解析式,构造新函数
的解析式,构造新函数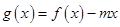 ,利用导数求出函数
,利用导数求出函数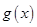 的极值,利用极值为零来求出参数
的极值,利用极值为零来求出参数 的值.
的值.
试题解析:(1)依题意, 的定义域为
的定义域为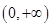 ,
,
当 ,
,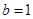 时,
时,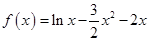 ,
, ,
,
由 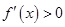 ,得
,得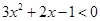 ,解得
,解得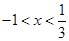 ;
;
由 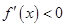 ,得
,得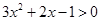 ,解得
,解得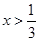 或
或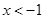 .
.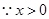 ,
, 在
在 单调递增,在
单调递增,在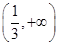 单调递减;
单调递减;
所以 的极大值为
的极大值为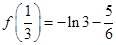 ,此即为最大值;
,此即为最大值;
(2)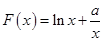 ,
,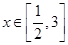 ,则有
,则有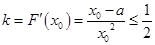 在
在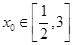 上有解,
上有解,
∴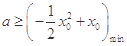 ,
,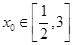
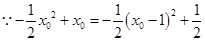 ,
,
所以当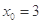 时,
时,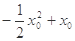 取得最小值
取得最小值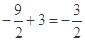 ,
,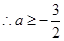 ;
;
(3)因为方程 有唯一实数解,所以
有唯一实数解,所以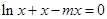 有唯一实数解,
有唯一实数解,
设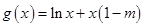 ,则
,则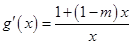 ,
,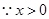 ,
, ,所以由
,所以由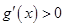 得
得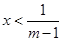 ,
,
由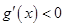 得
得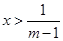 ,所以
,所以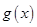 在
在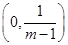 上单调递增,
上单调递增,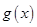 在
在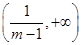 上单调递减,
上单调递减,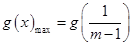 .
.
若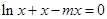 有唯一实数解,则必有
有唯一实数解,则必有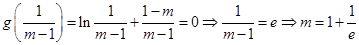 ,
,
所以当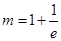 时,方程
时,方程 有唯一实数解.
有唯一实数解.
考点:1.利用导数求函数的最值;2.函数不等式恒成立;3.参数分离法;4.函数的零点

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
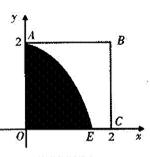
 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数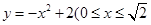 的图象,且点M到边OA距离为
的图象,且点M到边OA距离为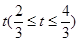 .
.
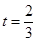 时,求直路
时,求直路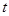 为何值时,地块OABC在直路
为何值时,地块OABC在直路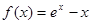 (
(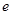 为自然对数的底)
为自然对数的底) 的最小值;
的最小值;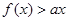 的解集为
的解集为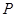 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
 .
. 在
在 处取得极大值,求实数
处取得极大值,求实数 的值;
的值; ,求
,求 上的最大值.
上的最大值.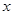 元/本(9≤
元/本(9≤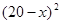 万本.
万本.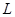 (万元)与每本书的定价
(万元)与每本书的定价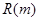 .
.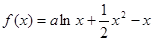
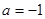 时,求函数
时,求函数 的单调区间;
的单调区间;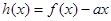 ,对定义域内任意x,均有
,对定义域内任意x,均有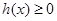 恒成立,求实数a的取值范围?
恒成立,求实数a的取值范围? ,
,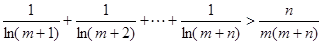 恒成立。
恒成立。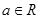 ,函数
,函数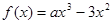 .
.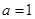 ,求函数
,求函数 的极值与单调区间;
的极值与单调区间;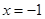 处的切线与直线
处的切线与直线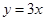 平行,求
平行,求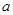 的值;
的值;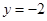 有三个公共点,求
有三个公共点,求