题目内容
16．
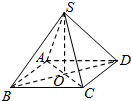如图，已知四棱锥S-ABCD的侧棱与底面边长都是2，且底面ABCD是正方形，则侧棱与底面所成的角（ ）| A． | 75° | B． | 60° | C． | 45° | D． | 30° |
分析 由条件利用正四棱锥的性质，利用直线和平面所成的角的定义找出侧棱与底面所成的角，再利用直角三角形中的边角关系，求得侧棱与底面所成的角．
解答 解：由于四棱锥S-ABCD的侧棱与底面边长都是2，故四棱锥S-ABCD为正四棱锥，设O为底面正方形的中心，
则∠SBO为侧棱与底面所成的角．
直角三角形SBO中，cos∠SBO=$\frac{OB}{SB}$=$\frac{\sqrt{2}}{2}$，∴∠SBO=45°，
故选：C．
点评 本题主要考查正四棱锥的性质，直线和平面所成的角，直角三角形中的边角关系，体现了转化的数学思想，属于中档题．
练习册系列答案
相关题目
7．
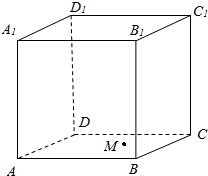如图所示，正方体ABCD-A1B1C1D1的棱长为a，平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等，则点M的轨迹为（ ）
如图所示，正方体ABCD-A1B1C1D1的棱长为a，平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等，则点M的轨迹为（ ）| A． | 直线 | B． | 椭圆 | C． | 抛物线 | D． | 双曲线 |
1．cos24°cos36°-sin24°cos54°=（ ）
| A． | cos12° | B． | sin12° | C． | $\frac{1}{2}$ | D． | $-\frac{1}{2}$ |
8．已知函数f（x）的定义域是R，f′（x）是f（x）的导数，f（1）=e，g（x）=f′（x）-f（x），g（1）=0，g（x）的导数恒大于零，函数h（x）=f（x）-ex（e=2.71828…是自然对数的底数）的最小值是（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
如图所示，已知正方体ABCD-A1B1C1D1，E、F分别是正方形A1B1C1D1和ADD1A1的中心，求EF和CD所成的角．
6．某化工厂生产一种化工产品，据负责该产品生产的部门预算，当该产品年产量在50吨至300吨之间时，其生产的总成本y（万元）与年产量x（吨）之间的部分对应数据大致如下表：
（1）给出如下四个函数：
①y=ax2+b，②y=$\frac{1}{10}{x}^{2}+ax+b$，③y=a•bx，④y=a•logbx．根据上表数据，从上述四个函数中选取一个最恰当的函数描述y与x的变化关系，并通过表中前两组数据，求出y与x的函数解析式；
（2）根据你求出的函数解析式，试问当年产量为多少吨时，生产每吨的平均成本最低？每吨的最低成本是多少？
（3）若将每吨产品的出厂价定为16万元，则年产量为多少吨时，方可使得全年的利润最大？并求出全年的最大利润．
| 生产量x（单位：吨） | 50 | 100 | 130 | 180 | 200 | 250 | 300 |
| 生产总成本y（单位：万元） | 2750 | 2000 | 1750 | 1800 | 2050 | 2750 | 4050 |
①y=ax2+b，②y=$\frac{1}{10}{x}^{2}+ax+b$，③y=a•bx，④y=a•logbx．根据上表数据，从上述四个函数中选取一个最恰当的函数描述y与x的变化关系，并通过表中前两组数据，求出y与x的函数解析式；
（2）根据你求出的函数解析式，试问当年产量为多少吨时，生产每吨的平均成本最低？每吨的最低成本是多少？
（3）若将每吨产品的出厂价定为16万元，则年产量为多少吨时，方可使得全年的利润最大？并求出全年的最大利润．