题目内容
直线3x+4y-9=0与圆(x-1)2+y2=1的位置关系是
- A.相离
- B.相切
- C.直线与圆相交且过圆心
- D.直线与圆相交但不过圆心
A
分析:由圆的标准方程找出圆心坐标和圆的半径r,再利用点到直线的距离公式求出圆心到已知直线的距离d,比较d与r的大小可得出直线与圆的位置关系,同时把圆心坐标代入直线方程,发现直线过圆心,即可得到正确的选项.
解答:由圆的方程(x-1)2+y2=1,得到圆心坐标为(1,0),半径r=1,
∵圆心到直线3x+4y-9=0的距离d=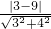 =
= >1=r,
>1=r,
∴直线与圆的位置关系是相离.
故选A
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,以及点与直线的位置关系,直线与圆的位置关系可以用d与r的大小来判断:当0≤d<r时,直线与圆相加;当d=r时,直线与圆相切;当d>r时,直线与圆相离.
分析:由圆的标准方程找出圆心坐标和圆的半径r,再利用点到直线的距离公式求出圆心到已知直线的距离d,比较d与r的大小可得出直线与圆的位置关系,同时把圆心坐标代入直线方程,发现直线过圆心,即可得到正确的选项.
解答:由圆的方程(x-1)2+y2=1,得到圆心坐标为(1,0),半径r=1,
∵圆心到直线3x+4y-9=0的距离d=
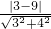 =
= >1=r,
>1=r,∴直线与圆的位置关系是相离.
故选A
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,以及点与直线的位置关系,直线与圆的位置关系可以用d与r的大小来判断:当0≤d<r时,直线与圆相加;当d=r时,直线与圆相切;当d>r时,直线与圆相离.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
设不等式组
所表示的平面区域是Ω1,平面区域是Ω2与Ω1关于直线3x-4y-9=0对称,对于Ω1中的任意一点A与Ω2中的任意一点B,|AB|的最小值等于( )
|
A、
| ||
| B、4 | ||
C、
| ||
| D、2 |
已知点P(x,y)的坐标满足条件
,那么点P到直线3x-4y-9=0的距离的最小值为( )
|
A、
| ||
B、
| ||
| C、2 | ||
| D、1 |