Question

设不等式组

x≥1 x-2y+3≥0 y≥x

所表示的平面区域是Ω₁，平面区域是Ω₂与Ω₁关于直线3x-4y-9=0对称，对于Ω₁中的任一点A与Ω₂中的任一点B，AB的最小值为

 

．

Answer 1

分析：根据已知的约束条件

x≥1 x-2y+3≥0 y≥x

画出满足约束条件的可行域Ω₁，根据对称的性质，不难得到：当A点距对称轴的距离最近时，|AB|有最小值．

解答：解：作出不等式组对应的平面区域Ω₁，（阴影部分CDE），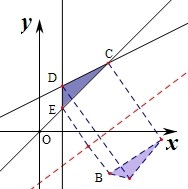
∵平面区域是Ω₂与Ω₁关于直线3x-4y-9=0对称，
∴要使AB的距离最小，则只需点A到直线3x-4y-9=0的距离最小即可，
由图象可知当点A位于点E时，A到直线3x-4y-9=0的距离最小，
由

x=1 y=x

，解得

x=1 y=1

，即E（1，1），
此时E到直线3x-4y-9=0的距离d=

|3-4-9|

32+42

=

10

5

=2，
∴AB的最小值为2d=2×2=4，
故答案为：4．

点评：利用线性规划解平面上任意两点的距离的最值，关键是要根据已知的约束条件，画出满足约束约束条件的可行域，再去分析图形，根据图形的性质、对称的性质等找出满足条件的点的坐标，代入计算，即可求解．