题目内容
已知 是定义在R上的不恒为零的函数,且对于任意的
是定义在R上的不恒为零的函数,且对于任意的 ,满足
,满足 ,
, ,
,
考查下列结论:① ;②
;② 为偶函数;③数列
为偶函数;③数列 为等比数列;④数列
为等比数列;④数列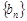 为等差数列.其中正确的是_________ .
为等差数列.其中正确的是_________ .
①③④
解析试题分析:令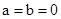 ,则
,则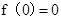 ,
,
令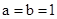 ,则
,则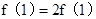 ,所以
,所以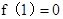 .
.
∴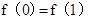 .故①正确.
.故①正确.
∵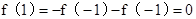 ,
,
∴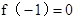 ,f(-x)=-f(x)+xf(-1)=-f(x),
,f(-x)=-f(x)+xf(-1)=-f(x),
∴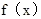 是R上的奇函数.故②不正确.
是R上的奇函数.故②不正确.
∵ ,∴
,∴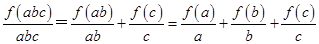 ,
,
以此类推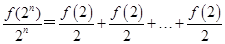 (共
(共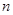 个)=
个)=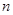 ,
,
∴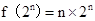 .∴
.∴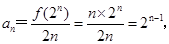 故③正确.
故③正确. ,故④正确.
,故④正确.
故答案为:①③④.
考点:数列的概念,抽象函数.

练习册系列答案
相关题目
 的定义域为_____________.
的定义域为_____________. ,其中
,其中 、
、 为常数,且
为常数,且 ,若
,若 为常数,则
为常数,则 的值为 .
的值为 . 的解所在区间为
的解所在区间为 ,则
,则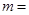 .
.
 ,则
,则 .
. 有三个不同的零点,则实数
有三个不同的零点,则实数 的取值范围是_____.
的取值范围是_____. 的值域为
的值域为 ,则
,则 的最大值为 .
的最大值为 . 则
则 的值等于 .
的值等于 . 是偶函数,直线
是偶函数,直线 与函数
与函数 的图象自左向右依次交于四个不同点
的图象自左向右依次交于四个不同点 ,
, ,
, ,
, .若
.若 ,则实数
,则实数 的值为 .
的值为 .