题目内容
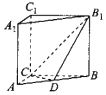
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,平面
为矩形,平面![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.

(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]()
![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(I)见解析; (II)![]() ; (Ⅲ)答案见解析 .
; (Ⅲ)答案见解析 .
【解析】
(Ⅰ)由题意结合三角形中位线的性质和线面平行的判定定理即可证得题中的结论;
(Ⅱ)由题意建立空间直角坐标系,求得半平面的法向量,然后结合法向量可得二面角的余弦值;
(Ⅲ)假设存在满足题意的点![]() ,由题意结合点的坐标和向量垂直的充分必要条件得到关于
,由题意结合点的坐标和向量垂直的充分必要条件得到关于![]() 的方程,解方程即可确定
的方程,解方程即可确定![]() 的值.
的值.
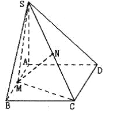
(I)设![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
因为底面![]() 是矩形,所以
是矩形,所以![]() 为
为![]() 中点 .
中点 .
又因为![]() 为
为![]() 中点 , 所以
中点 , 所以![]() ∥
∥![]() .
.
因为![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() .
.
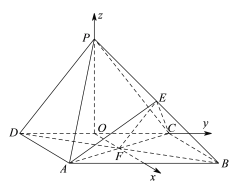
(II)取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() .
.
因为底面![]() 为矩形,所以
为矩形,所以![]() .
.
因为![]() ,
,![]() ,
,
所以![]() ∥
∥![]() ,所以
,所以![]() .
.
又因为平面PCD⊥平面ABCD,![]() 平面
平面![]() 平面PCD∩平面ABCD=CD.
平面PCD∩平面ABCD=CD.
所以PO⊥平面ABCD,
如图,建立空间直角坐标系![]() ,则
,则![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
, ![]()
所以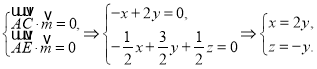
令![]() ,则
,则![]() ,所以
,所以![]() .
.
平面![]() 的法向量为
的法向量为![]() ,则
,则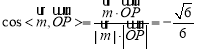 .
.
如图可知二面角![]() 为钝角,所以二面角
为钝角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(Ⅲ)在棱![]() 上存在点
上存在点![]() , 使
, 使![]() .
.
设![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() .
.
![]() .
.
因为![]() ,所以
,所以![]() .
.
所以![]() ,解得
,解得![]() .
.
所以在棱![]() 上存在点
上存在点![]() ,使
,使![]() ,且
,且![]() .
.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案【题目】某地区实施“光盘行动”以后,某自助啤酒吧也制定了自己的行动计划,进店的每一位客人需预交![]() 元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足
元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足![]() 升的,按
升的,按![]() 升计算(如剩余
升计算(如剩余![]() 升,记为剩余
升,记为剩余![]() 升).例如:结账时,某桌剩余酒量恰好为
升).例如:结账时,某桌剩余酒量恰好为![]() 升,则该桌的每位客人还应付
升,则该桌的每位客人还应付![]() 元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的
元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的![]() 组数据
组数据![]() (其中
(其中![]() 表示饮酒人数,
表示饮酒人数,![]() (升)表示饮酒量):
(升)表示饮酒量):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
剩余酒量(单位:升) |
|
|
|
|
|
结账时的倍率 |
|
|
|
|
|
(1)求由这![]() 组数据得到的
组数据得到的![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)小王约了![]() 位朋友坐在一桌饮酒,小王及朋友用量杯共量取了
位朋友坐在一桌饮酒,小王及朋友用量杯共量取了![]() 升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请
升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请![]() 位或
位或![]() 位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
参考数据:回归直线的方程是![]() ,其中
,其中 ,
,![]() .
.