Question

【题目】已知椭圆的离心率为.

（Ⅰ）求椭圆的方程；

（Ⅱ）设直线过点且与椭圆相交于两点.过点作直线的垂线，垂足为.证明直线过轴上的定点.

Answer 1

【答案】（1）；（2）见解析.

【解析】

（1）由离心率列方程可求得椭圆方程；

（2）当直线AB的斜率不存在时，直线BD过点（2，0）．当直线AB的斜率存在时，设直线AB为y=k（x-1），联立方程组，消去y整理得：（1+3k2）x2-6k2x+3k2-3=0．利用韦达定理、直线方程，结合已知条件求出直线BD过x轴上的定点．

（1）解：由题意可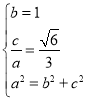得,解得，

所以椭圆C的方程为 ．

（2）直线BD恒过x轴上的定点N（2，0）．证明如下

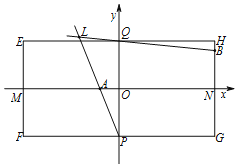
（a）当直线l斜率不存在时，直线l的方程为x=1，

不妨设A（1，），B（1，），D（3，）．

此时，直线BD的方程为：y=（x-2），所以直线BD过点（2，0）．

（b）当直线l的斜率存在时，设A（x1，y1），B（x2，y2），直线AB为y=k（x-1），D（3，y1）．

由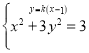得：（1+3k2）x2-6k2x+3k2-3=0．

所以x1+x2=，x1x2=．……（*）

直线BD：y-y1=（x-3），只需证明直线BD过点（2，0）即可.

令y=0，得x-3=，所以x===

即证，即证.

将（*）代入可得.

所以直线BD过点（2，0）

综上所述，直线BD恒过x轴上的定点（2，0）．