题目内容
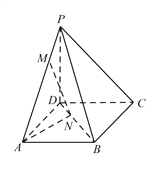
【题目】如图,四棱锥 ![]() 底面为正方形,已知
底面为正方形,已知 ![]() ,
,![]() ,点
,点 ![]() 为线段
为线段 ![]() 上任意一点(不含端点),点
上任意一点(不含端点),点 ![]() 在线段
在线段 ![]() 上,且
上,且 ![]() .
.
(1)求证:![]() ;
;
(2)若 ![]() 为线段
为线段 ![]() 中点,求直线
中点,求直线 ![]() 与平面
与平面 ![]() 所成的角的余弦值.
所成的角的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)延长![]() ,交
,交![]() 于点
于点![]() ,由相似三角形的性质可知
,由相似三角形的性质可知 ![]() ,从而得
,从而得![]() ,利用线面平行的判定定理可得直线
,利用线面平行的判定定理可得直线![]() 平面
平面![]() ;(2)由于
;(2)由于 ![]() ,
,![]() ,
,![]() 两两垂直,所以,以
两两垂直,所以,以![]() 为
为![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设 ![]() ,求出相关点的坐标及直线
,求出相关点的坐标及直线 ![]() 的方向向量,根据向量垂直数量积为零列方程组,求出平面
的方向向量,根据向量垂直数量积为零列方程组,求出平面 ![]() 的一个法向量,空间向量夹角余弦公式,可求解
的一个法向量,空间向量夹角余弦公式,可求解![]() 与平面
与平面 ![]() 夹角的正弦值,进而可求余弦值.
夹角的正弦值,进而可求余弦值.
试题解析:(1) 延长 ![]() ,交
,交 ![]() 于点
于点 ![]() ,连接
,连接 ![]() ,
,
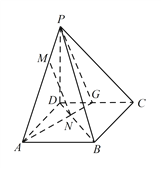
由相似知 ![]() ,可得:
,可得:![]() ,
,
![]() ,
,![]() ,
,
则 ![]() .
.
(2) 由于 ![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
以 ![]() ,
,![]() ,
,![]() 为
为 ![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
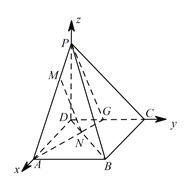
设 ![]() ,则
,则 ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则 ![]() ,平面
,平面 ![]() 的法向量为
的法向量为 ![]() ,
,
设向量 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() ,则
,则 ![]() ,
,
则 ![]() 与平面
与平面 ![]() 夹角的余弦值为
夹角的余弦值为 ![]() .
.
【方法点晴】本题主要考查线面平行的判定定理以及利用空间向量求线面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.

【题目】某P2P平台需要了解该平台投资者的大致年龄分布,发现其投资者年龄大多集中在区间[20,50]岁之间,对区间[20,50]岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 人数(单位:人) |
第一组 | [20,25) | 2 |
第二组 | [25,30) | a |
第三组 | [30,35) | 5 |
第四组 | [35,40) | 4 |
第五组 | [40,45) | 3 |
第六组 | [45,50] | 2 |

(Ⅰ)求a的值并画出频率分布直方图;
(Ⅱ)在统计表的第五与第六组的5人中,随机选取2人,求这2人的年龄都小于45岁的概率.
【题目】某公司经营一种二手机械,对该型号机械的使用年数![]() 与再销售价格
与再销售价格![]() (单位:百万元/台)进行统计整理,得到如下关系:
(单位:百万元/台)进行统计整理,得到如下关系:
使用年数 | 2 | 4 | 6 | 8 | 10 |
再销售价格 | 16 | 13 | 9.5 | 7 | 5 |
(1)求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() ;
;
(2)该机械每台的收购价格为![]() (百万元),根据(1)中所求的回归方程,预测
(百万元),根据(1)中所求的回归方程,预测![]() 为何值时,此公司销售一台该型号二手机械所获得的利润
为何值时,此公司销售一台该型号二手机械所获得的利润![]() 最大?
最大?
附:参考公式: ,
,![]() .
.