题目内容
已知数列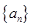 满足:
满足: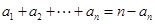 ,其中
,其中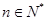 .
.
(1)求证:数列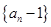 是等比数列;
是等比数列;
(2)令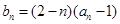 ,求数列
,求数列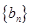 的最大项.
的最大项.
(1)详见解析;(2)最大项为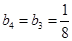 .
.
解析试题分析:(1)首先根据已知等式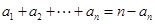 ,令
,令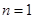 ,可得
,可得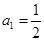 ,再根据已知等式可得
,再根据已知等式可得 ,将两式相减,即可得到数列
,将两式相减,即可得到数列 的一个递推公式,只需验证将此递推公式变形得到形如
的一个递推公式,只需验证将此递推公式变形得到形如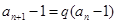 的形式,从可证明数列
的形式,从可证明数列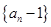 是等比数列;(2)由(1)可得
是等比数列;(2)由(1)可得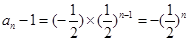 ,从而
,从而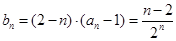 ,因此要求数列
,因此要求数列 的最大项,可以通过利用作差法判断数列
的最大项,可以通过利用作差法判断数列 的单调性来求得:
的单调性来求得: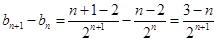 ,
,
当 时,
时,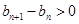 ,即
,即 ;当
;当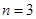 时,
时,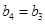 ; 当
; 当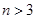 时,
时, ,即
,即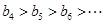 ,因此数列
,因此数列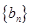 的最大项为
的最大项为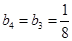 .
.
试题解析:(1)当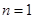 时,
时,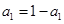 ,∴
,∴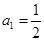 , 1分
, 1分
又∵ , 2分
, 2分
∴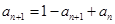 ,即
,即 ,∴
,∴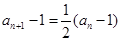 . 4分
. 4分
又∵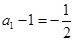 ,∴数列
,∴数列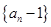 是首项为
是首项为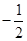 ,公比为
,公比为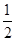 的等比数列; 6分
的等比数列; 6分
(2)由(1)知,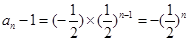 ,
,
∴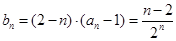 , ∴
, ∴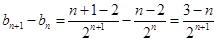 , 8分
, 8分
当 时,
时,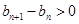 ,即
,即 , 9分
, 9分
当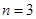 时,
时,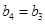 , 10分
, 10分
当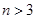 时,
时, ,即
,即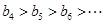 , 11分
, 11分
∴数列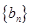 的最大项为
的最大项为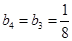 , 13分
, 13分
考点:1.数列的通项公式;2.数列的单调性判断.

练习册系列答案
相关题目

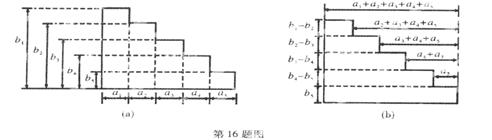
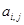 ,且满足
,且满足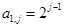 ,
,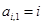 ,
, (
(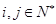 );又记第3行的数3,5,8,13,22,39……为数列{bn},则
);又记第3行的数3,5,8,13,22,39……为数列{bn},则
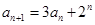 ,(n∈N﹡),且
,(n∈N﹡),且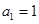 ,则数列{an}的通项公式为 .
,则数列{an}的通项公式为 .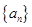 的通项公式为
的通项公式为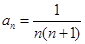 ,则该数列的前100项和为_________.
,则该数列的前100项和为_________. (
(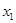 ,
,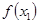 ),
), (
( ,
,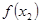 )是函数
)是函数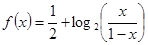 的图象上的任意两点.
的图象上的任意两点.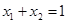 时,求
时,求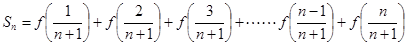 ,其中
,其中 ,求
,求
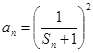 ,其中
,其中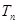 为数列
为数列 的前
的前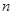 项和,求证
项和,求证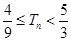 .
. 的前n项和为
的前n项和为 ,
, ,且
,且 (
( ),数列
),数列 满足
满足 ,
, ,对任意
,对任意 。
。 .
. ;
; ,不等式
,不等式 恒成立,试求实数λ的取值范围.
恒成立,试求实数λ的取值范围.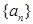 满足
满足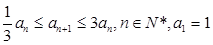 .
.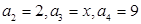 ,求
,求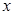 的取值范围;
的取值范围;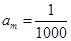 ,正整数
,正整数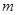 的最小值,以及
的最小值,以及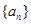 的仅比;
的仅比;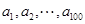 成等差数列,求数列
成等差数列,求数列 的前n项和为Sn,已知
的前n项和为Sn,已知 ,且
,且 对一切
对一切 都成立.
都成立.