题目内容
设数列{an}满足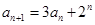 ,(n∈N﹡),且
,(n∈N﹡),且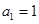 ,则数列{an}的通项公式为 .
,则数列{an}的通项公式为 .
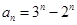
解析试题分析:因为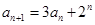 ,两边同除以
,两边同除以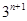 ,得
,得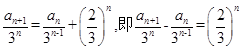 ,令
,令 ,则
,则 ,
,
所以 ,以上n-1个式子相加,得
,以上n-1个式子相加,得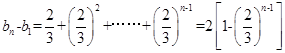 ,即
,即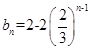 ,所以
,所以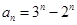 。
。
考点:数列通项公式的求法;等比数列的前n项和。
点评:若已知的递推式形如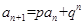 求数列的通项公式,常用的方法是:等式的两边同除以
求数列的通项公式,常用的方法是:等式的两边同除以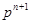 ,构造新数列,然后用累加法。
,构造新数列,然后用累加法。

练习册系列答案
相关题目
题目内容
设数列{an}满足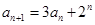 ,(n∈N﹡),且
,(n∈N﹡),且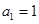 ,则数列{an}的通项公式为 .
,则数列{an}的通项公式为 .
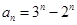
解析试题分析:因为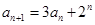 ,两边同除以
,两边同除以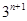 ,得
,得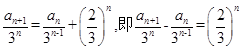 ,令
,令 ,则
,则 ,
,
所以 ,以上n-1个式子相加,得
,以上n-1个式子相加,得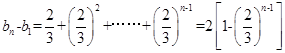 ,即
,即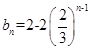 ,所以
,所以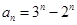 。
。
考点:数列通项公式的求法;等比数列的前n项和。
点评:若已知的递推式形如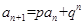 求数列的通项公式,常用的方法是:等式的两边同除以
求数列的通项公式,常用的方法是:等式的两边同除以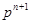 ,构造新数列,然后用累加法。
,构造新数列,然后用累加法。
