题目内容
【题目】正四面体ABCD中,M是棱AD的中点,O是点A在底面BCD内的射影,则异面直线BM与AO所成角的余弦值为____.
【答案】![]()
【解析】
取BC中点E,DC中点F,连结DE、BF,则由题意得DE∩BF=O,取OD中点N,连结MN,则MN∥AO,从而∠BMN是异面直线BM与AO所成角(或所成角的补角),由此能求出异面直线BM与AO所成角的余弦值.
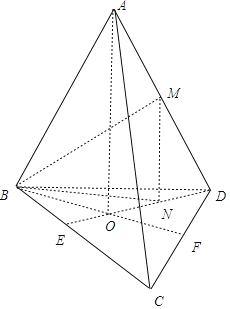
取BC中点E,DC中点F,连结DE、BF,则由题意得DE∩BF=O,
取OD中点N,连结MN,则MN∥AO,
∴∠BMN是异面直线BM与AO所成角(或所成角的补角),
设正四面体ABCD的棱长为2,由![]() ,
,
∴![]() ,
,
∵O是点A在底面BCD内的射影,MN∥AO,∴MN⊥平面BCD,
∴![]() ,
,
∴异面直线BM与AO所成角的余弦值为![]() .
.
故答案为:![]() .
.

【题目】柴静《穹顶之下》的播出,让大家对雾霾天气的危害有了更进一步的认识,对于雾霾天气的研究也渐渐活跃起来,某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据:
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测燃放烟花爆竹的天数为![]() 的雾霾天数.
的雾霾天数.

【题目】某车间为了给贫困山区的孩子们赶制一批爱心电子产品,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下表所示:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 |
| 3 | 4 |
|
经统计发现零件个数![]() 与加工时间
与加工时间![]() 具有线性相关关系.
具有线性相关关系.
(1)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)试预测加工10个零件需要多少时间.
利用公式: ,
,![]()
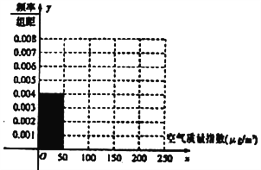
【题目】全世界越来越关注环境保护问题,某监测站点于2018年1月某日起连续![]() 天监测空气质量指数(
天监测空气质量指数(![]() ),数据统计如下:
),数据统计如下:
空气质量指数( |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 |
| 10 | 5 |
(1)根据所给统计表和频率分布直方图中的信息求出![]() ,
,![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
(2)由频率分布直方图,求该组数据的众数和中位数;
(3)在空气质量指数分别属于![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取
的监测数据中,用分层抽样的方法抽取![]() 天,再从中任意选取
天,再从中任意选取![]() 天,求事件
天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.