题目内容
6．函数f（x）=x2+3x+2在区间（-5，5）上的最大值、最小值分别是（ ）| A． | 42，12 | B． | 42，-$\frac{1}{4}$ | ||
| C． | 12，-$\frac{1}{4}$ | D． | 无最大值，有最小值是-$\frac{1}{4}$ |
分析 由f（x）的对称轴为x=-$\frac{3}{2}$可知f（x）=x2+3x+2在区间（-5，5）上先减后增，利用单调性即可求出最小值，由于定义域为开区间，故无最大值．
解答 解：∵f（x）=x2+3x+2图象开口向上，对称轴为x=-$\frac{3}{2}$，
∴f（x）在（-5，-$\frac{3}{2}$]上单调递减，在（-$\frac{3}{2}$，5）上单调递增．
∴当x=-$\frac{3}{2}$时，f（x）取得最小值f（-$\frac{3}{2}$）=-$\frac{1}{4}$；
∵（-5，5）为开区间，故f（x）无最大值．
点评 本题考查了二次函数在给定区间上的最值，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
16．已知集合A={1，2，4}，B={x|x2=1}，那么A∪B=（ ）
| A． | {1} | B． | {1，2，4} | C． | {-1，1，2，4} | D． | {2，4} |
17．
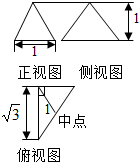某几何体的三视图如图所示，则它的外接球的体积为（ ）
某几何体的三视图如图所示，则它的外接球的体积为（ ）| A． | 4π | B． | $\frac{8}{3}π$ | C． | $\frac{4}{9}π$ | D． | $\frac{4}{3}π$ |
11．已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（b＞a＞0）的正半轴焦点为F，负半轴焦点为F′，AA′为长轴，点Q为椭圆上任意一点，则分别以|QF|，|QF′|，|AA′|为直径的圆之间的位置关系说法正确的是（ ）
| A． | 以|QF|为直径的圆与以|AA′|为直径的圆内切 | |
| B． | 以|QF′|为直径的圆与以|AA′|为直径的圆相交 | |
| C． | 以|QF|为直径的圆与以|AA′|为直径的圆相交 | |
| D． | 以|QF|为直径的圆与以|QF′|为直径的圆相切 |
18．设A={x|3x+6=0}，则A=（ ）
| A． | -2 | B． | {2} | C． | {-2} | D． | 2∈A |