题目内容
【题目】已知集合A={x|y=lg(x-![]() )},B={x|
)},B={x|![]() -cx<0,c>0},若AB,则实数c的取值范围是( )
-cx<0,c>0},若AB,则实数c的取值范围是( )
A.(0,1]B.[1,+∞)
C.(0,1)D.(1,+∞)
【答案】B
【解析】
A集合用对数的真数的定义即可求出范围,B集合化简后含有参数,所以,画出数轴,用数轴表示AB,即可求出c的取值范围.
解法1:A={x|y=lg(x-![]() )}={x|x-
)}={x|x-![]() >0}={x|0<x<1},B={x|
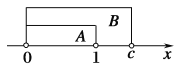
>0}={x|0<x<1},B={x|![]() -cx<0,c>0}={x|0<x<c},因为AB,画出数轴,如图所示,得c≥1.
-cx<0,c>0}={x|0<x<c},因为AB,画出数轴,如图所示,得c≥1.
解法2:因为A={x|y=lg(x-![]() )}={x|x-
)}={x|x-![]() >0}={x|0<x<1},取c=1,则B={x|0<x<1},所以AB成立,故可排除C,D;取c=2,则B={x|0<x<2} ,所以AB成立,故可排除A,故选B.
>0}={x|0<x<1},取c=1,则B={x|0<x<1},所以AB成立,故可排除C,D;取c=2,则B={x|0<x<2} ,所以AB成立,故可排除A,故选B.

练习册系列答案
相关题目