题目内容
【题目】在正方体![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点
的中点
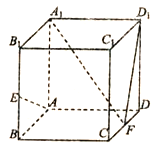
(1)求证:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 面
面![]() ,若存在,试确定
,若存在,试确定![]() 的值,若不存在说明理由;
的值,若不存在说明理由;
(3)在(2)的条件下,求面![]() 与面
与面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(1)详见解析(2)存在,![]() (3)
(3)![]()
【解析】
(1) 取AB中点N,连接A1N,FN,可证得AE垂直于A1N,而A1NFD是平行四边形,可得到AE垂直于![]() ,再由A1D1 AE可得到线面垂直;(2)取A1B1中点G,取GB1中点M,连接GB,ME,MC1,通过证明线线平行即
,再由A1D1 AE可得到线面垂直;(2)取A1B1中点G,取GB1中点M,连接GB,ME,MC1,通过证明线线平行即![]() ME可得到线面平行;(3)建立坐标系,求得两个面的法向量,先得到余弦值,进而得到二面角的正弦值.
ME可得到线面平行;(3)建立坐标系,求得两个面的法向量,先得到余弦值,进而得到二面角的正弦值.
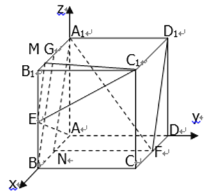
(1)证明:取AB中点N,连接A1N,FN,
在正方体AC1中,AN![]() FD,所以四边形ANFD为平行四边形,AD
FD,所以四边形ANFD为平行四边形,AD![]() FN,
FN,
因为A1D1![]() AD,所以A1D1
AD,所以A1D1![]() FN,所以四边形A1NFD1为平行四边形,A1N
FN,所以四边形A1NFD1为平行四边形,A1N![]() FD1
FD1
在正方形A1B1BA中,RtEBA≌RtNAA1,所以∠EAB=∠NA1A
因为∠A1NA +∠NA1A=90°所以∠A1NA +∠EAB =90°,AEA1N,AE FD1
A1D1面A1B1BA,AE面A1B1BA,所以A1D1 AE,所以AE面A1FD1。
(2) 取A1B1中点G,取GB1中点M,连接GB,ME,MC1,
A1G![]() BN,所以四边形A1GBN为平行四边形,A1N
BN,所以四边形A1GBN为平行四边形,A1N![]() BG
BG
E为B1B的中点,M点为A1B1的四等分点,
所以EM∥BG,EM∥FD1
FD1面C1ME,EM面C1ME,所以D1F//面C1ME,
此时![]() =
=![]()
(3)如图分别以AB、AD、AA1为x、y、z轴建立空间坐标系,
则E(2,0,1),C1(2,2,2),M(![]() ,0,2), A1(0,0,2), D1(0,2,2), F(1,2,0)
,0,2), A1(0,0,2), D1(0,2,2), F(1,2,0)
![]() =(
=(![]() ,2,0)
,2,0) ![]() =(0,2,1)
=(0,2,1) ![]() =(0,2,0)
=(0,2,0) ![]() =(-1,0,2)
=(-1,0,2)
设面MEC1的法向量为![]() =(x,y,z)
=(x,y,z)
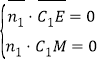 得
得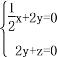 令y=1,则x=4,z=2,
令y=1,则x=4,z=2, ![]() =(4,1,2)
=(4,1,2)
设面![]() 的法向量为
的法向量为![]() =(x,y,z)
=(x,y,z)
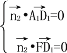 得
得![]() y=0令z=1,则x=2,
y=0令z=1,则x=2, ![]() =(2,0,1)
=(2,0,1)
cos<![]()
![]() >=
>=![]() =
=![]() =
=![]()
设面A1FD1与面C1ME所成二面角为θ,则|cosθ|=|cos<![]()
![]() >|=
>|=![]()
所以sinθ=![]() =
=![]()

 春雨教育同步作文系列答案
春雨教育同步作文系列答案【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关注的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在[25,30),[55,60)的被调查者中赞成“延迟退休”的人数分别是3人和2人.现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(I)求年龄在[25,30)的被调查者中选取的2人都赞成“延迟退休”的概率;
(II)若选中的4人中,不赞成“延迟退休”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.

【题目】某种蔬菜从1月1日起开始上市,通过市场调查,得到该蔬菜种植成本![]() (单位:元/
(单位:元/![]() )与上市时间
)与上市时间![]() (单位:10天)的数据如下表:
(单位:10天)的数据如下表:
时间 | 5 | 11 | 25 |
种植成本 | 15 | 10.8 | 15 |
(1)根据上表数据,从下列函数:![]() ,
,![]() ,
,![]() ,
,![]() 中(其中
中(其中![]() ),选取一个合适的函数模型描述该蔬菜种植成本
),选取一个合适的函数模型描述该蔬菜种植成本![]() 与上市时间
与上市时间![]() 的变化关系;
的变化关系;
(2)利用你选取的函数模型,求该蔬菜种植成本最低时的上市时间及最低种植成本.