题目内容
【题目】某种蔬菜从1月1日起开始上市，通过市场调查，得到该蔬菜种植成本
（单位：元/
）与上市时间
（单位：10天）的数据如下表：
时间 | 5 | 11 | 25 |
种植成本 | 15 | 10.8 | 15 |
（1）根据上表数据，从下列函数：
，
，
，
中（其中
），选取一个合适的函数模型描述该蔬菜种植成本与上市时间的变化关系；
（2）利用你选取的函数模型，求该蔬菜种植成本最低时的上市时间及最低种植成本.
【答案】（1）
；（2）该蔬菜上市150天时，该蔬菜种植成本最低为10（元/
）.
【解析】
（1）先作出散点图，根据散点图的分布即可判断只有模型
符合，然后将数据代入建立方程组，求出参数
.
（2）由于模型为二次函数，结合定义域，利用配方法即可求出最低种植成本以及对应得上市时间.
解：（1）以上市时间
（单位：10天）为横坐标，以种植成本
（单位/）为纵坐标，画出散点图（如图）.
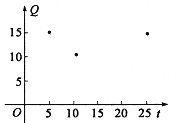
根据点的分布特征，
，
，
这三个函数模型与表格所提供的数据不吻合，只有函数模型与表格所提供的数据吻合最好，
所以选取函数模型进行描述该蔬菜种植成本与上市时间的变化关系.
将表格所提供的三组数据分别代入，
得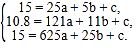
解得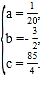
所以，描述该蔬菜种植成本与上市时间的变化关系的函数为
.
（2）由（1）知
，
所以当
时，的最小值为10，
即该蔬菜上市150天时，该蔬菜种植成本最低为10（元/）.
练习册系列答案
名校课堂系列答案
相关题目
