题目内容
已知等差数列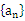 的首项
的首项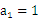 ,公差
,公差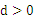 ,且第2项、第5项、第14项分别是等比数列
,且第2项、第5项、第14项分别是等比数列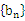 的第2项、第3项、第4项。
的第2项、第3项、第4项。
①求数列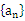 与
与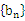 的通项公式;
的通项公式;
②设数列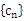 对
对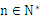 均有
均有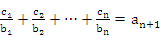 成立,求
成立,求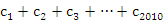 +
+ 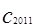
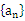 的首项
的首项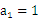 ,公差
,公差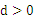 ,且第2项、第5项、第14项分别是等比数列
,且第2项、第5项、第14项分别是等比数列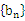 的第2项、第3项、第4项。
的第2项、第3项、第4项。①求数列
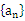 与
与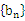 的通项公式;
的通项公式;②设数列
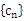 对
对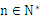 均有
均有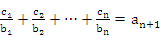 成立,求
成立,求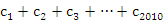 +
+ 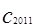
(1)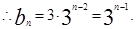 (2)
(2)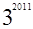
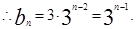 (2)
(2)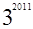
(1)利用等差数列和等比数列的概念及性质易求两个数列的通项公式;(2)先求出数列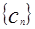 的通项公式,然后再利用分组求和及等比数列的前N项和公式求出数列的前2011项和
的通项公式,然后再利用分组求和及等比数列的前N项和公式求出数列的前2011项和
(1)由已知有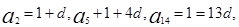
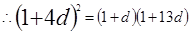 ,
,
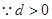 ,解得
,解得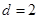
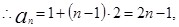 …………………3分
…………………3分
又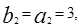
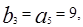
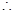 数列
数列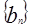 的公比为3.
的公比为3. 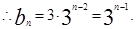 …………………5分
…………………5分
(2)由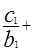
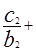 …
…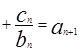 得,当
得,当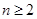 时,
时,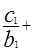
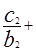 …
…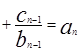
两式相减得,当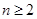 时,
时,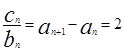 ,
,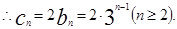 …………………8分
…………………8分
又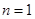 时,
时,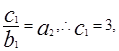
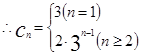 ,…………………10分
,…………………10分
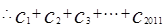 =3+
=3+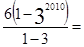 3-3+
3-3+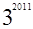 =
=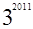 。…………………12分
。…………………12分
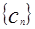 的通项公式,然后再利用分组求和及等比数列的前N项和公式求出数列的前2011项和
的通项公式,然后再利用分组求和及等比数列的前N项和公式求出数列的前2011项和(1)由已知有
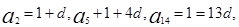
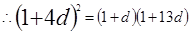 ,
,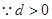 ,解得
,解得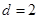
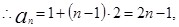 …………………3分
…………………3分又
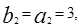
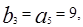
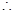 数列
数列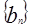 的公比为3.
的公比为3. 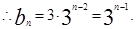 …………………5分
…………………5分(2)由
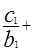
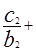 …
…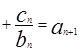 得,当
得,当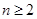 时,
时,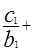
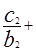 …
…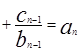
两式相减得,当
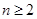 时,
时,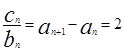 ,
,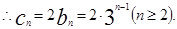 …………………8分
…………………8分又
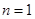 时,
时,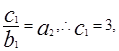
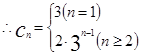 ,…………………10分
,…………………10分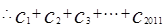 =3+
=3+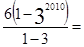 3-3+
3-3+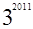 =
=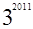 。…………………12分
。…………………12分
练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
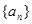 是等差数列,
是等差数列,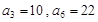 ,数列
,数列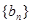 的前n项和是
的前n项和是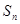 ,且
,且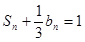 .(1)求数列
.(1)求数列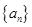 的通项公式
的通项公式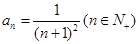 ,
,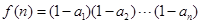 ,试通过计算
,试通过计算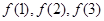 的值,推测出
的值,推测出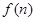 的值。
的值。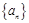 ,其前
,其前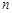 项的和为
项的和为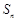 ,且
,且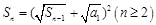 ,若
,若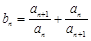 ,且数列
,且数列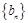 的前
的前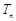 ,则
,则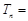 .
.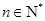 ,
,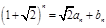 (
(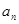 、
、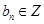 ).
).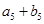 的值; (2)求证:数列
的值; (2)求证:数列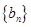 各项均为奇数.
各项均为奇数.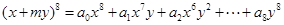 ,若
,若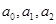 成公差大于0的等差数列,(1)求
成公差大于0的等差数列,(1)求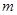 的值;(2)求
的值;(2)求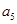 的值;(3)求
的值;(3)求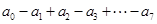 的值.
的值.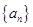 满足
满足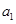 =1,且
=1,且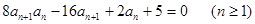
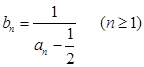
 、
、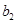 、
、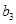 的值;
的值;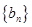 的通项公式;
的通项公式;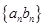 的前
的前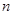 项和
项和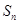 .
.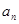 }的前n项和
}的前n项和
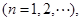 其中a、b是非零常数,则存在数列{
其中a、b是非零常数,则存在数列{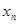 }、{
}、{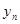 }使得( )
}使得( )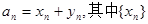 为等差数列,{
为等差数列,{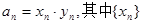 为等差数列,{
为等差数列,{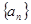 为等差数列,
为等差数列,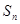 为其前n项和,且
为其前n项和,且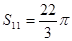 ,则
,则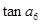 的值是( )
的值是( )