题目内容
设Sn为等差数列{an}的前n项和，已知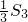
与
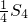的等比中项为
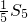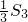，已知与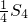的等差中项为1．
（1）求等差数列{an}的通项；
（2）求数列{|an|}的前n项和Tn．
解：（1）由已知得：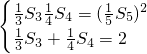
，…（2分）
设等差数列{an}的首项为a1，公差为d，则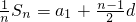
，
代入上述不等式组得：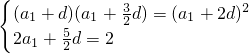
…（4分）
解得：
或
…（6分）
故
或an=1…（7分）
（2）若an=1，则Tn=n，…（8分）
若，令an≥0，得：n≤2；…（10分）
故当n≤2时，
，…（12分）
当n＞2时，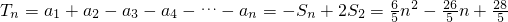
…（15分）
分析：（1）由已知得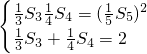：，利用等差数列的求和公式，代入可求a1，d，，进而可求通项an
（2）结合（1）中的条件可求数列{an}的和，进而根据n的取值范围可求Tn
点评：本题主要考查了等差数列的性质及求和公式的应用，其中（2）要注意分类讨论思想的应用．
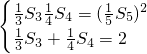，…（2分）设等差数列{an}的首项为a1，公差为d，则
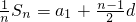，代入上述不等式组得：
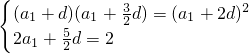…（4分）解得：
或…（6分）故
或an=1…（7分）（2）若an=1，则Tn=n，…（8分）
若
，令an≥0，得：n≤2；…（10分）故当n≤2时，
，…（12分）当n＞2时，
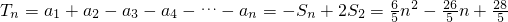…（15分）分析：（1）由已知得：
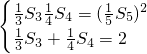，利用等差数列的求和公式，代入可求a1，d，，进而可求通项an（2）结合（1）中的条件可求数列{an}的和，进而根据n的取值范围可求Tn
点评：本题主要考查了等差数列的性质及求和公式的应用，其中（2）要注意分类讨论思想的应用．
练习册系列答案
名校课堂系列答案
相关题目
设Sn为等差数列{an}的前n项和，若S8=30，S4=7，则a4的值等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|