题目内容
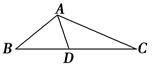
如图所示,AB是☉O的直径,弦BD、CA的延长线相交于点E,F为BA延长线上一点,且BD·BE=BA·BF,求证:
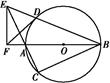
(1)EF⊥FB;
(2)∠DFB+∠DBC=90°.

(1)EF⊥FB;
(2)∠DFB+∠DBC=90°.
见解析
证明:(1)连接AD.
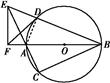
在△ADB和△EFB中,
∵BD·BE=BA·BF,
∴
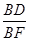 =
=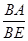 .
.又∠DBA=∠FBE,
∴△ADB∽△EFB,
又∵AB为☉O直径,
∴∠EFB=∠ADB=90°,即EF⊥FB.
(2)由(1)知∠ADB=∠ADE=90°,∠EFB=90°,
∴E、F、A、D四点共圆,
∴∠DFB=∠AEB.
又AB是☉O的直径,则∠ACB=90°,
∴∠DFB+∠DBC=∠AEB+∠DBC=90°.

练习册系列答案
相关题目
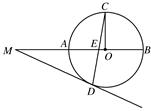
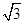 ,求MA及CE的长.
,求MA及CE的长.
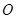 的直径
的直径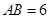 ,
, 为圆周上一点,
为圆周上一点, ,过
,过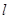 ,则点
,则点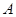 到直线
到直线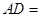 ___________.
___________.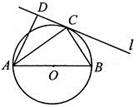

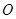 的弦ED,CB的延长线交于点A,若BD
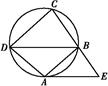
的弦ED,CB的延长线交于点A,若BD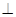 AE,AB=4,BC=2,AD=3,则CE= ;
AE,AB=4,BC=2,AD=3,则CE= ; 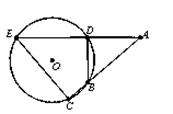

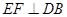 ,垂足为F,若
,垂足为F,若 ,
,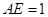 ,则
,则