题目内容
已知函数f(x)=
-
(a>0,x>0).
(1)判断函数f(x)在(0,+∞)上的单调性;
(2)若f(x)在[
,2]上的值域是[
,2],求a的值.
| 1 |
| a |
| 1 |
| x |
(1)判断函数f(x)在(0,+∞)上的单调性;
(2)若f(x)在[
| 1 |
| 2 |
| 1 |
| 2 |
(1)函数f(x)在(0,+∞)上单调递增.
设x1>x2>0,f(x1)-f(x2)=(
-
)-(
-
)=
-
=
因为x1>x2>0,所以x1-x2>0,x1•x2>0,所以f(x1)-f(x2)>0,
所以f(x1)>f(x2),因此函数f(x)在(0,+∞)上是单调递增的.
(2)由(1)知函数f(x)在[
,2]上单调递增,并且f(x)在[
,2]上的值域是[
,2],
所以
,所以a=
.
设x1>x2>0,f(x1)-f(x2)=(
| 1 |
| a |
| 1 |
| x1 |
| 1 |
| a |
| 1 |
| x2 |
| 1 |
| x2 |
| 1 |
| x1 |
| x1-x2 |
| x1•x2 |
因为x1>x2>0,所以x1-x2>0,x1•x2>0,所以f(x1)-f(x2)>0,
所以f(x1)>f(x2),因此函数f(x)在(0,+∞)上是单调递增的.
(2)由(1)知函数f(x)在[
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以
|
| 2 |
| 5 |

练习册系列答案
相关题目
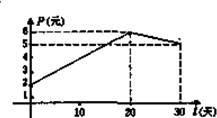
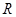 上的函数
上的函数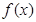 ,有下述四个命题;
,有下述四个命题;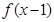 的图像关于点
的图像关于点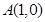 对称;
对称;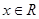 ,有
,有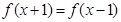 ,则
,则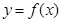 的图像关于直线
的图像关于直线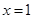 对称;
对称;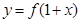 与函数
与函数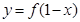 的图像关于直线
的图像关于直线