题目内容
已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是( )
| A．22πR2 | B． πR2 | C． πR2 | D． πR2 |
B
如图所示为组合体的轴截面,
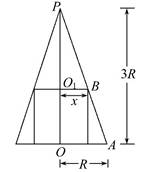
由相似三角形的比例关系,得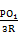
=
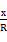,PO1=3x,圆柱的高为3R-3x,
所以圆柱的全面积为S=2πx2
+2πx(3R-3x)=-4πx2+6πRx,
则当x=
R时,S取最大值,
Smax=πR2.
由相似三角形的比例关系,得
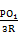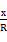=,PO1=3x,圆柱的高为3R-3x,所以圆柱的全面积为S=2πx2
+2πx(3R-3x)=-4πx2+6πRx,
则当x=
R时,S取最大值,Smax=
πR2.
练习册系列答案
百年学典课时学练测系列答案
相关题目
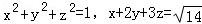，则x+y+z= _________ ．
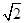的正四棱柱的各顶点均在同一个球面上，则该球的体积为（ ）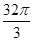
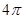
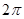
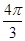
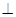平面ABCD，则点A1的轨迹是（ ）
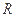的球面，两个截面圆的半径为
，
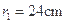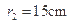．两截面间的距离为
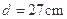，求球的表面积（ ）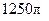
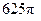
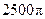
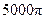
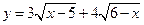的最大值。