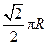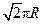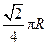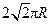题目内容
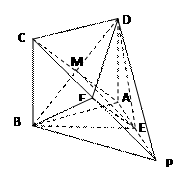
如图,四棱锥P-ABCD中,底面ABCD为正方形,DA⊥面ABP,AB=1,PA=2,∠PAB=600,E为PA的中点,F为PC上不同于P、C的任意一点.
(1)求证:PC∥面EBD
(2)求异面直线AC与PB间的距离
(3)求三棱锥E-BDF的体积.
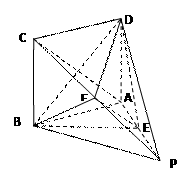
(1)求证:PC∥面EBD
(2)求异面直线AC与PB间的距离
(3)求三棱锥E-BDF的体积.

(1)见解析
(2)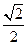
(3)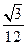
(2)
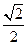
(3)
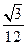
(1)设AC交BD于M,连接ME
∵面ABCD为正方形,∴M为AC的中点
又E为PA的中点,∴ME∥PC
∵ME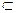 面EBD,∴PC∥面EBD
面EBD,∴PC∥面EBD
(2)∵面ABCD为正方形, ∴BD⊥AC
∵AB=1,PA=2,∠PAB=600,∴在△PAB中,由余弦定理得
PB2=PA2+AB2-2AB·PAcos600=4+1-2×1×2×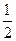 =3
=3
∴PA2=PB2+AB2,即AB⊥PB
∵DA⊥面ABP,CB∥DA
∴CB⊥面ABP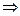 CB⊥PB ,∴PB⊥面ABCD,∴PB⊥MB,即MB为异面直线AC与PB间的垂线段
CB⊥PB ,∴PB⊥面ABCD,∴PB⊥MB,即MB为异面直线AC与PB间的垂线段
∵DB=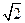
∴异面直线AC与PB间的距离为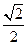
(3)由(2)知,PB、BC、AB两两互相垂直.如图建立空间直角坐标系,
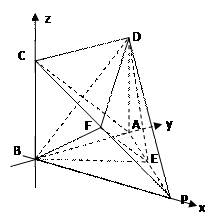
则A(0,1,0),P(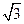 ,0,0),C(0,0,1),D(0,1,1)
,0,0),C(0,0,1),D(0,1,1)
∵E为PA的中点,∴E(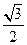 ,
,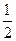 ,0)
,0)
设面BED的法向量为n=(a,b,c)
则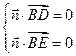
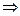
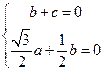
令c=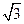 ,则b=-
,则b=-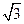 ,a=1
,a=1 n=(1,-
n=(1,-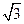 ,
,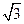 )
)
由(1)知,PC∥面EBD,所以C点到面EBD的距离与F点到面EBD的距离相等.
设向量n与向量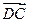 所成的角为
所成的角为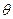
则cos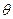 =
=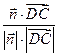 =
=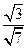
设C点到面EBD的距离为d
则d=DC×cos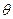 =
=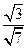
由题设条件可求得DE=DB=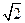 ,BE=1
,BE=1
∴S△DEB=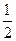 ×1×
×1×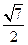 =
=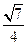
∴VE-BDF=VF-EBD=VC-EBD=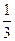 ×
×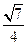 ×
×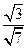 =
=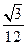

∵面ABCD为正方形,∴M为AC的中点
又E为PA的中点,∴ME∥PC
∵ME
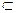 面EBD,∴PC∥面EBD
面EBD,∴PC∥面EBD(2)∵面ABCD为正方形, ∴BD⊥AC
∵AB=1,PA=2,∠PAB=600,∴在△PAB中,由余弦定理得
PB2=PA2+AB2-2AB·PAcos600=4+1-2×1×2×
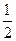 =3
=3∴PA2=PB2+AB2,即AB⊥PB
∵DA⊥面ABP,CB∥DA
∴CB⊥面ABP
 CB⊥PB ,∴PB⊥面ABCD,∴PB⊥MB,即MB为异面直线AC与PB间的垂线段
CB⊥PB ,∴PB⊥面ABCD,∴PB⊥MB,即MB为异面直线AC与PB间的垂线段∵DB=
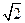
∴异面直线AC与PB间的距离为
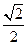
(3)由(2)知,PB、BC、AB两两互相垂直.如图建立空间直角坐标系,

则A(0,1,0),P(
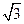 ,0,0),C(0,0,1),D(0,1,1)
,0,0),C(0,0,1),D(0,1,1)∵E为PA的中点,∴E(
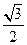 ,
,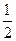 ,0)
,0)设面BED的法向量为n=(a,b,c)
则
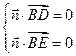
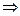
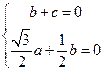
令c=
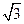 ,则b=-
,则b=-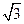 ,a=1
,a=1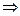 n=(1,-
n=(1,-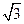 ,
,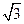 )
)由(1)知,PC∥面EBD,所以C点到面EBD的距离与F点到面EBD的距离相等.
设向量n与向量
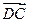 所成的角为
所成的角为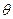
则cos
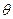 =
=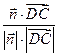 =
=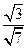
设C点到面EBD的距离为d
则d=DC×cos
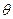 =
=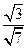
由题设条件可求得DE=DB=
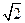 ,BE=1
,BE=1∴S△DEB=
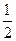 ×1×
×1×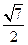 =
=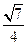
∴VE-BDF=VF-EBD=VC-EBD=
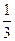 ×
×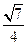 ×
×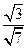 =
=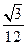

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
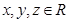 ,且
,且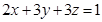 ,则
,则 的最小值是 .
的最小值是 .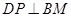 ,则点P的轨迹周长为( ).
,则点P的轨迹周长为( ).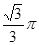
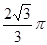
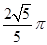
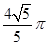
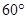 的共有( )
的共有( ) πR2
πR2 πR2
πR2 πR2
πR2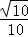

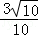
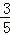
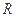 ,球面上
,球面上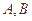 两点都在北纬45°圈上,它们的球面距离为
两点都在北纬45°圈上,它们的球面距离为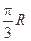 ,
,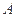 点在东经30°上,则
点在东经30°上,则