��Ŀ����
11����������C����ƽ���ϵĶ���P0���������Ե�P0Ϊ����ĽǦ���ʹ�æ��ݡ�AP0B��������C�ϵ�����������ͬ�ĵ�A��B���������ƽǦ�Ϊ����C����ڵ�P0�ġ���ǡ�������������С�ġ���ǡ�Ϊ����C����ڵ�P0�ġ�ȷ��ǡ�������C��y=$\left\{\begin{array}{l}\sqrt{{x^2}+1}��x��0��\\ 2-\sqrt{1-{x^2}}��x��0��\end{array}$���������ԭ��O�ġ�ȷ��ǡ��Ĵ�С��$\frac{5��}{12}$������ ��������f��x����ͼ����O��������ֱ�����������ӽ���x��0ʱ������y=$\sqrt{{x}^{2}+1}$��ֱ��y=k1x���ӽ������ǽ����ߣ����k1=1��x��0ʱ�����߿ɻ�Ϊx2+��y-2��2=1��x��0����Բ�ĵ�ֱ�ߵľ���Ϊ$\frac{2}{\sqrt{{{k}_{2}}^{2}+1}}$=1����k2=-$\sqrt{3}$��������ֱ�ߵļнǹ�ʽ���ɵõ�����ġ�ȷ��ǡ���
��� 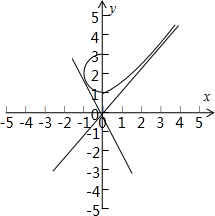 �⣺��������f��x����ͼ����O��������ֱ�����������ӽ��������ǵķ��̷ֱ�Ϊy=k1x��y=k2x��
�⣺��������f��x����ͼ����O��������ֱ�����������ӽ��������ǵķ��̷ֱ�Ϊy=k1x��y=k2x��
��x��0ʱ������y=$\sqrt{{x}^{2}+1}$��ֱ��y=k1x���ӽ�����Ϊ˫���ߵĽ����ߣ���k1=1��
��x��0ʱ�����߿ɻ�Ϊx2+��y-2��2=1��x��0����Բ�ĵ�ֱ�ߵľ���Ϊ$\frac{2}{\sqrt{{{k}_{2}}^{2}+1}}$=1����k2=-$\sqrt{3}$��
����ֱ�ߵļнǹ�ʽ�ã�tan��=|$\frac{1+\sqrt{3}}{1-\sqrt{3}}$|=2+$\sqrt{3}$��
������C����ڵ�O�ġ�ȷ��ǡ�Ϊ$\frac{5��}{12}$��
�ʴ�Ϊ��$\frac{5��}{12}$��
���� ���⿼���¶��塰ȷ��ǡ���Ӧ�ã�����ֱ����Բ��λ�ù�ϵ��˫���ߵ����ʣ������ߣ������е��⣮

��ϰ��ϵ�д�
�����Ŀ
2��������f��x��=sin��x+$\frac{��}{6}$����ͼ���ϸ���������겻�䣬����������ԭ����2��������ͼ���һ���Գ��᷽�̿����ǣ�������
| A�� | $x=-\frac{��}{12}$ | B�� | $x=\frac{��}{12}$ | C�� | $x=\frac{��}{3}$ | D�� | $x=\frac{2��}{3}$ |
19����֪��2x2+4x+3��6=a0+a1��x+1��2+a2��x+1��4+��+a6��x+1��12����a0+a2+a4+a6��ֵΪ��������
| A�� | $\frac{{3}^{6}-1}{2}$ | B�� | $\frac{{3}^{6}+1}{2}$ | C�� | $\frac{{3}^{6}+2}{2}$ | D�� | $\frac{{3}^{6}-2}{2}$ |
20������z=$\frac{2+i}{3-i}$��ʵ�����鲿֮��Ϊ��������
| A�� | 0 | B�� | $\frac{1}{2}$ | C�� | 1 | D�� | 2 |