题目内容
20．复数z=$\frac{2+i}{3-i}$的实部与虚部之和为（ ）| A． | 0 | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
分析 利用复数的运算法则、实部与虚部的定义即可得出．
解答 解：复数z=$\frac{2+i}{3-i}$=$\frac{（2+i）（3+i）}{（3-i）（3+i）}$=$\frac{5+5i}{10}$=$\frac{1}{2}+\frac{1}{2}i$，
∴实部与虚部之和=$\frac{1}{2}+\frac{1}{2}$=1，
故选：C．
点评 本题考查了复数的运算法则、实部与虚部的定义，属于基础题．
练习册系列答案
相关题目
10．设△ABC的内角A，B，C所对边的长分别a，b，c，若b+c=2a，3sinA=5sinB，则角C=（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{3π}{4}$ | C． | $\frac{5π}{6}$ | D． | $\frac{2π}{3}$ |
8．已知角α的终边与以坐标原点为圆心，以1为半径的圆交于点P（sin$\frac{2π}{3}$，cos$\frac{2π}{3}$），则角α的最小正值为（ ）
| A． | $\frac{5π}{6}$ | B． | $\frac{2π}{3}$ | C． | $\frac{5π}{3}$ | D． | $\frac{11π}{6}$ |
15．设Sn为等比数列{an}的前n项和，8a2+a5=0，则$\frac{{S}_{6}}{{S}_{3}}$等于（ ）
| A． | -11 | B． | -7 | C． | 5 | D． | 11 |
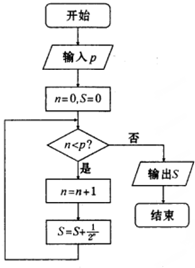
9．执行如图的程序框图，则输出的值P=（ ）
| A． | 12 | B． | 10 | C． | 8 | D． | 6 |
如图，长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2，点E是棱AB上一点