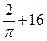题目内容
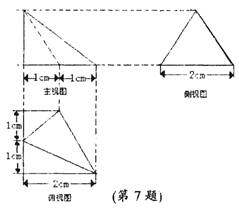
在三棱锥A—BCD中,已知侧面ABD 底面BCD,若
底面BCD,若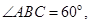
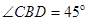 ,则侧棱AB与底面BCD所成的角为( )
,则侧棱AB与底面BCD所成的角为( )
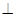 底面BCD,若
底面BCD,若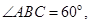
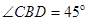 ,则侧棱AB与底面BCD所成的角为( )
,则侧棱AB与底面BCD所成的角为( )A.30 | B.45 | C.60 | D.75 |
B
利用三面角公式,求出侧棱AB与底面BCD所成的角即可.
解:由题意在三棱锥A-BCD中,已知侧面ABD⊥底面BCD,侧棱AB在底面BCD上

的射影为DB,由三面角公式可得:
cos60°=cos45°cos∠ABD.
所以cos∠ABD= .
.
∠ABD=45°
故选B.
解:由题意在三棱锥A-BCD中,已知侧面ABD⊥底面BCD,侧棱AB在底面BCD上

的射影为DB,由三面角公式可得:
cos60°=cos45°cos∠ABD.
所以cos∠ABD=
 .
.∠ABD=45°
故选B.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
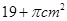
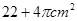
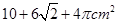
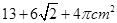
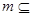 平面
平面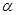 ,则条件甲:直线
,则条件甲:直线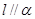 是条件乙:
是条件乙: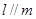 的
的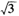 B.
B.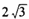
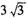 D
D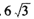
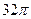


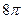


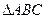 的三个顶点均在球
的三个顶点均在球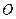 的球面上,且
的球面上,且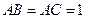 ,
,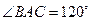 ,直线
,直线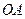 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为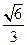 ,则球面上
,则球面上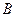 、
、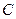 两点间的球面距离为________
两点间的球面距离为________ 的侧面展开图是边长为4的正方形,则圆柱的表面积是 ( )
的侧面展开图是边长为4的正方形,则圆柱的表面积是 ( ) .
.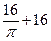 B.
B. C.
C. D.
D.