题目内容
【题目】“冰桶挑战赛”是一项社交网络上发起的慈善公益活动,活动规定:被邀请者要么在![]() 小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外
小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外![]() 个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(1)若某参与者接受挑战后,对其他![]() 个人发出邀请,则这
个人发出邀请,则这![]() 个人中至少有
个人中至少有![]() 个人接受挑战的概率是多少?
个人接受挑战的概率是多少?
(2)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下列联表:
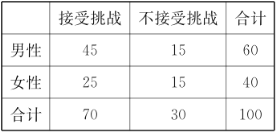
根据表中数据,能否有![]() %的把握认为“冰桶挑战赛与受邀者的性别有关”?
%的把握认为“冰桶挑战赛与受邀者的性别有关”?
附: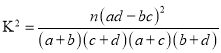

【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
试题(1)分别列出3人参加活动的所以可能结果,和其中至少有3人接受挑战的情况种数,然后根据古典概型的概率计算;(2)根据列联表中的数据计算观测值![]() ,然后和表中的
,然后和表中的![]() 进行比较,大于就表示有关,小于表示没有90%的把握认为“冰桶挑战赛与受邀者的性别有关”.
进行比较,大于就表示有关,小于表示没有90%的把握认为“冰桶挑战赛与受邀者的性别有关”.
试题解析:(1)这![]() 个人接受挑战分别记为
个人接受挑战分别记为![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() 分别表示这
分别表示这![]() 个人不接受挑战.
个人不接受挑战.
这![]() 个人参与该项活动的可能结果为:
个人参与该项活动的可能结果为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共有
,共有![]() 种.
种.
其中,至少有![]() 个人接受挑战的可能结果有:
个人接受挑战的可能结果有:![]() ,
,![]() ,
,![]() ,
,![]() ,共有
,共有![]() 种.
种.
根据古典概型的概率公式,所求的概率为![]() .
.
(2)根据![]() 列联表,得到
列联表,得到![]() 的观测值为:
的观测值为:

![]() .
.
因为![]() .
.
所以没有![]() %的把握认为“冰桶挑战赛与受邀者的性别有关”.
%的把握认为“冰桶挑战赛与受邀者的性别有关”.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案【题目】某市A,B,C,D四所中学报名参加某高校2015年自主招生考试的学生人数如下表所示:
中学 | A | B | C | D |
人数 | 40 | 30 | 10 | 20 |
该市教委为了解参加考试的学生的学习状况,采用分层抽样的方法从四所中学报名参加考试的学生中随机抽取50名参加问卷调查.则A,B,C,D四所中学抽取的学生人数分别为( )
A.15,20,10,5B.15,20,5,10
C.20,15,10,5D.20,15,5,10