题目内容
【题目】设函数f(x)在(-∞,+∞)上有意义,且对于任意的x,y∈R,有|f(x)-f(y)|<|x-y|并且函数f(x+1)的对称中心是(-1,0),若函数g(x)-f(x)=x,则不等式g(2x-x2)+g(x-2)<0的解集是( ).
A.![]() B.
B.![]()
C.![]() ,
,![]() D.
D.![]()
【答案】A
【解析】
由已知可知f(x)为奇函数,从而可得g(-x)也为奇函数,然后结合|f(x)-f(y)|<|x-y|,得 ![]() ,从而可得g(x)单调递增,结合单调性及奇函数的定义可求.
,从而可得g(x)单调递增,结合单调性及奇函数的定义可求.
由函数f(x+1)的对称中心是(-1,0),可得f(x)的图象关于(0,0)对称即f(x)为奇函数,
∴f(-x)=-f(x),
∵g(x)-f(x)=x,
∴g(x)=f(x)+x,
∴g(-x)=f(-x)-x=-f(x)-x=-g(x),
∵对于任意的x,y∈R,有|f(x)-f(y)|<|x-y|,
∴|g(x)-g(y)-(x-y)|<|x-y|,
∴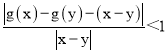 ,
,
即|![]() |<1,
|<1,
∴0<![]() <2,
<2,
由对任意实数![]() 有
有![]() 得g(x)单调递增,
得g(x)单调递增,
∵g(2x-x2)+g(x-2)<0,
∴g(2x-x2)<-g(x-2)=g(2-x),
∴2x-x2<2-x,
整理可得,x2-3x+2>0,
解可得,x>2或x<1,
故选:A.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目