题目内容
(13分) 已知数列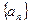 中
中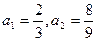 .当
.当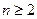 时
时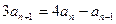 .(
.(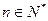 )
)
(Ⅰ)证明: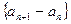 为等比数列;
为等比数列;
(Ⅱ) 求数列
求数列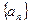 的通项;
的通项;
(Ⅲ)若数列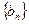 满足
满足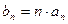 ,求
,求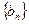 的前
的前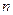 项和
项和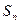 .
.
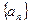 中
中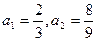 .当
.当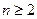 时
时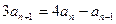 .(
.(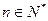 )
)(Ⅰ)证明:
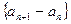 为等比数列;
为等比数列;(Ⅱ)
 求数列
求数列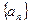 的通项;
的通项;(Ⅲ)若数列
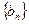 满足
满足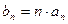 ,求
,求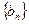 的前
的前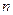 项和
项和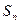 .
.(1)略
(2)
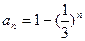
(3)
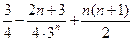
(Ⅰ)证明: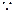 数列
数列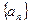 中
中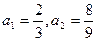 .当
.当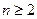 时
时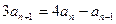 .(
.(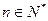 )
)
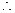 当
当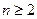 时
时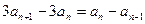 ,即
,即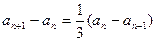 .
.
所以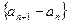 是以
是以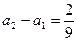 为首项,以
为首项,以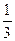 为公比的等比数列
为公比的等比数列
(Ⅱ)解:由(Ⅰ)知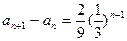 ,故
,故 ,
,
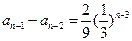 ,…
,…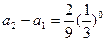 ,
,
累加得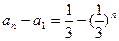 ,所以
,所以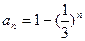 .
.
(Ⅲ)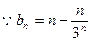 ,
,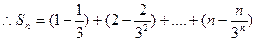 =
=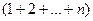
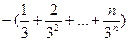 =
=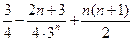 .
.
 数列
数列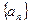 中
中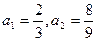 .当
.当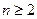 时
时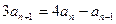 .(
.(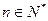 )
)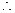 当
当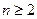 时
时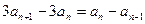 ,即
,即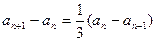 .
.所以
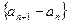 是以
是以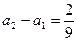 为首项,以
为首项,以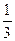 为公比的等比数列
为公比的等比数列(Ⅱ)解:由(Ⅰ)知
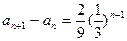 ,故
,故 ,
,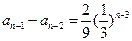 ,…
,…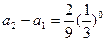 ,
,累加得
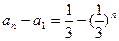 ,所以
,所以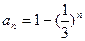 .
.(Ⅲ)
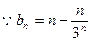 ,
,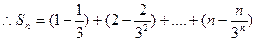 =
=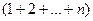
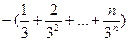 =
=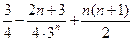 .
.
练习册系列答案
相关题目
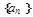 中,
中,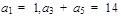 ,其前n项和
,其前n项和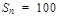 ,则n等于( )
,则n等于( ) 中,
中,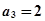 ,
, ,若
,若 为等差数列,则
为等差数列,则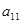 =( )。
=( )。

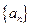 满足:
满足: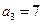 ,
,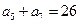 .
.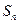 .
.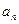 及
及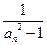 (n
(n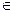 N*),求数列
N*),求数列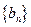 的前n项和
的前n项和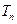
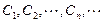 是坐标平面上的一列圆,它们的圆心都在
是坐标平面上的一列圆,它们的圆心都在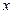 轴的正半轴上,且都与直线
轴的正半轴上,且都与直线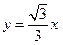 相切,对每一个正整数
相切,对每一个正整数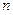 ,圆
,圆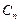 都与圆
都与圆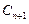 相互外切,以
相互外切,以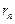 表示
表示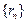 为递增数列.
为递增数列.
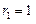 ,求数列
,求数列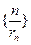 的前
的前 的公差大于0,且
的公差大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前n项的和为
的前n项的和为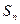 ,且
,且 .
. ,求证:
,求证: .
.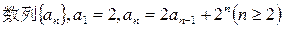
 ;
;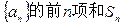 ;
;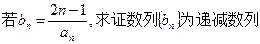 。
。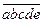 称为“凸”数,当且仅当它满足a<b<c,c>d>e(如12430,13531等), 则在所有的五位数中“凸”数的个数是( ▲ )
称为“凸”数,当且仅当它满足a<b<c,c>d>e(如12430,13531等), 则在所有的五位数中“凸”数的个数是( ▲ ) 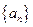 是等差数列,若
是等差数列,若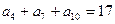 ,
,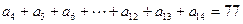 且
且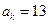 ,则
,则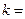 _________
_________