题目内容
【题目】在直四棱柱ABCD﹣A1B1C1D1中，底面ABCD为菱形，E，F分别是BB1 ， DD1的中点，G为AE的中点且FG=3，则△EFG的面积的最大值为（ ）
A.
B.3
C.
D.
【答案】B
【解析】解：连接AC交BD于O，
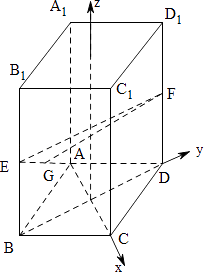
∵底面ABCD是菱形，∴AC⊥BD，
以OC，OD，OZ为坐标轴建立空间直角坐标系O﹣xyz，
设OC=a，OD=b，棱柱的高为h，
则A（﹣a，0，0），E（0，﹣b， 
），F（0，b， ），∴G（﹣ 
，﹣ 
， 
）．
=（﹣ ，﹣ 
，﹣ ）， 
=（0，﹣2b，0），
∴cos＜ 
＞= 
= 
= ，
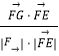∴E到直线FG的距离d=| |sin＜ ＞=2b 
=b 
，
∴S△EFG= 
= 
= 
≤ 
× 
=3．当且仅当b2=4﹣b2即b2=2时取等号．
故选：B．
【考点精析】通过灵活运用棱柱的结构特征，掌握两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形即可以解答此题．
灵星计算小达人系列答案
【题目】某大学为调研学生在A，B两家餐厅用餐的满意度，从在A，B两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分．整理评分数据，将分数以10为组距分成6组：[0，10），[10，20），[20，30），[30，40），[40，50），[50，60]，得到A餐厅分数的频率分布直方图，和B餐厅分数的频数分布表：
B餐厅分数频数分布表 | |
分数区间 | 频数 |
[0，10） | 2 |
[10，20） | 3 |
[20，30） | 5 |
[30，40） | 15 |
[40，50） | 40 |
[50，60] | 35 |
（Ⅰ）在抽样的100人中，求对A餐厅评分低于30的人数；
（Ⅱ）从对B餐厅评分在[0，20）范围内的人中随机选出2人，求2人中恰有1人评分在[0，10）范围内的概率；
（Ⅲ）如果从A，B两家餐厅中选择一家用餐，你会选择哪一家？说明理由．
