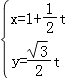题目内容
【题目】已知两定点F1（﹣ 
，0），F2（ ，0），满足条件|PF2|﹣|PF1|=2的点P的轨迹是曲线E．
（1）求曲线E的方程；
（2）设过点（0，﹣1）的直线与曲线E交于A，B两点．如果|AB|=6 
，求直线AB的方程．
【答案】
（1）解：由双曲线的定义可知，曲线E是以F1（﹣ 
，0），F2（ ，0）为焦点的双曲线的左支，且c= ，a=1，
∴b= 
=1，故曲线E的方程为x2﹣y2=1（x＜0）
（2）解：设A（x1，y1），B（x2，y2），由题意建立方程组 
，消去y，得（1﹣k2）x2+2kx﹣2=0，
又已知直线与双曲线左支交于两点A，B，有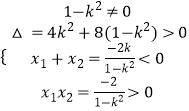 
，
解得﹣ ＜k＜﹣1．
∵|AB|= 
= 
=2 
= 
，
∴28k4﹣55k2+25=0，
∴ 
或 
，
∵﹣ ＜k＜﹣1，
∴ 
，
∴直线AB的方程为 
【解析】（1）根据条件|PF2|﹣|PF1|=2，利用双曲线的定义，可求曲线E的方程；（2）直线方程代入双曲线方程，利用直线与双曲线左支交于两点A，B，求出k的范围，再利用|AB|=6 
，求出k的值，从而可求直线AB的方程．
练习册系列答案
相关题目
