题目内容
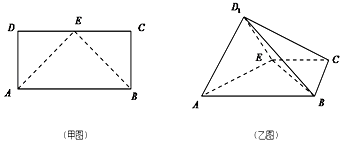
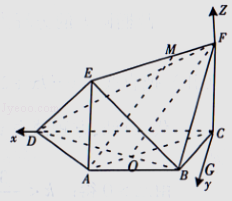
【题目】如图,在梯形ABCD中,AB∥DC,AD=AB=BC=1, ![]() ,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=1,点M在线段EF上.
,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=1,点M在线段EF上. 
(1)当 ![]() 为何值时,AM∥平面BDF?证明你的结论;
为何值时,AM∥平面BDF?证明你的结论;
(2)求二面角B﹣EF﹣D的平面角的余弦值.
【答案】
(1)解:当 ![]() 时,AM∥平面BDF.
时,AM∥平面BDF.
证明如下:
在梯形ABCD中,设AC∩BD=O,连接FO,
因为AD=BC=1,∠ADC=60°,
所以DC=2,又AB=1,
因为△AOB∽△CDO,
因此CO:AO=2:1,
所以 ![]() ,因为ACFE是矩形,
,因为ACFE是矩形,
所以四边形AOFM是平行四边形,
所以AM∥OF,
又OF平面BDF,AM平面BDF,
所以AM∥平面BDF
(2)解:在平面ABCD内过点C作GC⊥CD,
因为平面ACFE⊥平面ABCD,且交线为AC,
则CF⊥平面ABCD,即CF⊥GC,CF⊥DC,
以点C为原点,分别以CD,CG,CF所在直线为x,y,z轴,建立空间直角坐标系,
则 ![]() ,D(2,0,0),
,D(2,0,0), ![]() ,F(0,0,1),
,F(0,0,1),
所以 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设平面BEF的法向量为 ![]() ,则
,则 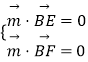 ,
,
∴ 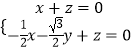 ,取
,取 ![]() ,
,
同理可得平面DEF的法向量 ![]() ,
,
所以 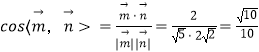 ,
,
因为二面角B﹣EF﹣D是锐角,所以其余弦值是 ![]() .
.
【解析】(1)当 ![]() 时,设AC∩BD=O,连接FO,推导出四边形AOFM是平行四边形,从而AM∥OF,由此能证明AM∥平面BDF.(2)在平面ABCD内过点C作GC⊥CD,以点C为原点,分别以CD,CG,CF所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角B﹣EF﹣D的余弦值.
时,设AC∩BD=O,连接FO,推导出四边形AOFM是平行四边形,从而AM∥OF,由此能证明AM∥平面BDF.(2)在平面ABCD内过点C作GC⊥CD,以点C为原点,分别以CD,CG,CF所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角B﹣EF﹣D的余弦值.
【考点精析】掌握直线与平面平行的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.