题目内容
【题目】已知CD是等边三角形ABC的AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
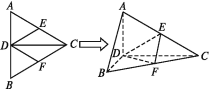
(1)求直线BC与平面DEF所成角的余弦值;
(2)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)以D为原点建立空间直角坐标系,设等边三角形ABC的边长为![]() ,可得直线BC的方向向量
,可得直线BC的方向向量![]() 和平面EDF的法向量
和平面EDF的法向量![]() =(3,-
=(3,-![]() ,3),设直线BC与平面DEF所成角为
,3),设直线BC与平面DEF所成角为![]() ,则有
,则有![]() ,然后再求出
,然后再求出![]() ,即为所求.(2)假设在线段BC上存在一点,使得AP⊥DE,则由
,即为所求.(2)假设在线段BC上存在一点,使得AP⊥DE,则由![]() =
=![]() 可得P
可得P![]() ,于是
,于是![]() ,由
,由![]() 可得
可得![]() ,符合题意,进而得到结论.
,符合题意,进而得到结论.
(1)以点D为坐标原点,直线DB,DC分别为x轴,y轴,建立空间直角坐标系,
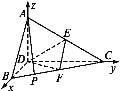
设等边三角形ABC的边长为a,则A![]() ,B
,B![]() ,C
,C![]() ,E
,E![]() ,F
,F![]() ,
,
设平面EDF的法向量为![]() ,
,
则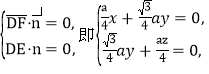
取![]() =(3,-
=(3,-![]() ,3).
,3).
又因为![]() ,
,
设直线BC与平面DEF所成角为![]() ,
,
则![]() ,
,
所以![]() ,
,
即直线BC与平面DEF所成角的余弦值等于![]() .
.
(2)假设在线段BC上存在一点,使AP⊥DE,
令![]() =
=![]() ,
,
即![]() =λ
=λ![]() ,
,
则P![]() ,
,
于是![]() .
.
因为AP⊥DE,
所以![]() ,
,
整理得![]() λa2-
λa2-![]() a2=0,
a2=0,
解得![]() ,符合题意.
,符合题意.
故线段BC上存在一点P,使AP⊥DE.

练习册系列答案
相关题目