题目内容
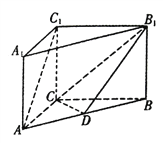
【题目】在三棱柱 ![]() 中,底面为正三角形,侧棱垂直底面,
中,底面为正三角形,侧棱垂直底面, ![]() .若
.若 ![]() 分别是棱
分别是棱 ![]() 上的点,且
上的点,且 ![]() ,则异面直线
,则异面直线 ![]() 与
与 ![]() 所成角的余弦值为( )
所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】
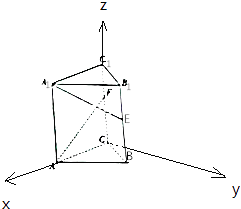
以 ![]() 为原点,
为原点, ![]() 为
为 ![]() 轴,在平面
轴,在平面 ![]() 中过作
中过作 ![]() 的垂线为
的垂线为 ![]() 轴,
轴, ![]() 为
为 ![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系, ![]() 在三棱柱
在三棱柱 ![]() 中,底面为正三角形,侧棱垂直底面,
中,底面为正三角形,侧棱垂直底面, ![]() ,
, ![]() 分别是棱
分别是棱 ![]() 上的点,且
上的点,且 ![]() ,
, ![]()
![]() , 设异面直线
, 设异面直线 ![]() 与
与 ![]() 所成角所成角为
所成角所成角为 ![]() , 则
, 则 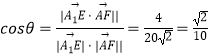 .所以异面直线
.所以异面直线 ![]() 与
与 ![]() 所成角的余弦值为
所成角的余弦值为 ![]() .
.
所以答案是:D.
【考点精析】认真审题,首先需要了解异面直线及其所成的角(异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系),还要掌握用空间向量求直线间的夹角、距离(已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则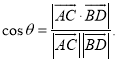 )的相关知识才是答题的关键.
)的相关知识才是答题的关键.

【题目】某同学参加学校自主招生3门课程的考试,假设该同学第一门课程取得优秀成绩概率为 ![]() ,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
ξ | 0 | 1 | 2 | 3 |
p |
| x | y |
|
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率及求p,q的值;
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.
【题目】某个体服装店经营某种服装,在某周内获得的纯利润y(单位:元)与该周每天销售这种服装的件数x之间的一组数据关系如下表:
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(1)求纯利润y与每天销售件数x之间的回归方程;
(2)若该周内某天销售服装20件,估计可获得纯利润多少元?
已知:![]() =280,
=280,![]() xiyi=3 487,
xiyi=3 487,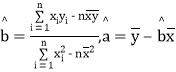 .
.