题目内容
【题目】记![]()
![]() .
.
(1)求方程![]() 的实数根;
的实数根;
(2)设![]() ,
,![]() ,
,![]() 均为正整数,且
均为正整数,且![]() 为最简根式,若存在
为最简根式,若存在![]() ,使得
,使得![]() 可唯一表示为
可唯一表示为![]() 的形式
的形式![]() ,试求椭圆
,试求椭圆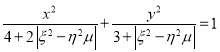 的焦点坐标;
的焦点坐标;
(3)已知![]() ,是否存在
,是否存在![]() ,使得
,使得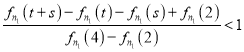 成立,若存在,试求出
成立,若存在,试求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)2(2)![]() ,
,![]() .(3)不存在.见解析
.(3)不存在.见解析
【解析】
(1)根据函数解析式化简方程![]() ,求解即可;(2)要求椭圆焦点坐标,应先求
,求解即可;(2)要求椭圆焦点坐标,应先求![]() 的值,因为
的值,因为![]() ,由二项展开可得
,由二项展开可得![]() ,这里
,这里![]() ,
,![]() ,为了得到
,为了得到![]() ,先得
,先得![]() ,相乘得
,相乘得![]() ,再结合条件
,再结合条件![]() ,进而可求得
,进而可求得![]() ,可得结果;
,可得结果;
(3)不存在![]() ,使得
,使得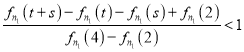 成立,即证对任意
成立,即证对任意![]() ,都有
,都有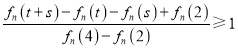 ,由条件可得即证在
,由条件可得即证在![]() 下,不等式
下,不等式![]() 恒成立.
恒成立.
方法一,当![]() 时,不等式恒成立易证;当
时,不等式恒成立易证;当![]() ,且
,且![]() 时,用二项式定理展开,然后缩小可证不等式恒成立;方法二,用数学归纳法证明;方法三,由已知可设
时,用二项式定理展开,然后缩小可证不等式恒成立;方法二,用数学归纳法证明;方法三,由已知可设![]() ,由
,由![]() 可得
可得![]() ,将不等式的左边化简为
,将不等式的左边化简为![]()
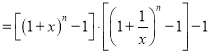 ,利用二项式定理展开缩小可证。
,利用二项式定理展开缩小可证。
解:(1)由![]() 得,
得,![]()
∵![]() ,∴
,∴![]()
∴![]() ,即所求方程的实数根为2.
,即所求方程的实数根为2.
(2)因为![]() 为最简根式,且
为最简根式,且![]() ,
,![]() ,
,![]() ,所以由二项展开可得
,所以由二项展开可得
![]() ,这里
,这里![]() ,
,![]() ,
,
则![]() .
.
两式相乘得![]() .
.
即![]() ,
,
现由![]() ,
,
又依题意得:![]() ,便知
,便知![]() ,
,
知由(*)得![]() ,即
,即![]() .
.
因此,椭圆方程为![]() ,
,
故,其焦点坐标为![]() ,
,![]() .
.
(3)不存在.
只须证:对任意![]() ,都有
,都有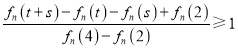 .
.
证明如下,由![]()
可得![]() ,
,
注意到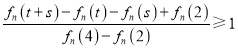
![]() ,
,
故亦只须证:在![]() 下,
下,
不等式![]() 恒成立.
恒成立.
方法一:∵![]() ,
,![]() ,
,
∴由已知可得![]() 从而
从而![]() .
.
当![]() 时,因
时,因![]() ,
,![]() ,
,
故![]() 成立.
成立.
当![]() ,且
,且![]() 时,
时,
![]()
![]() …
…
![]()
![]()
![]()
![]() .
.
综上,![]() 对一切
对一切![]() 成立.
成立.
方法二:∵![]() ,
,![]() ,
,
∴![]() ,从而
,从而![]() ,
,
因此![]()
(i)当![]() 时,因
时,因![]() ,
,![]() ,
,
故![]() 成立.
成立.
(ii)假设当![]() 时,不等式成立,即
时,不等式成立,即![]()
那么,当![]() 时,注意到
时,注意到![]() ,
,![]() ,故
,故
![]()
![]()
![]() ,
,
![]()
即![]() 成立,这就是说,当
成立,这就是说,当![]() 时,不等式
时,不等式![]() 也成立.
也成立.
综上所述,不等式![]() 对一切
对一切![]() 成立.
成立.
方法三:由已知可设![]() ,由
,由![]() 可得
可得![]() ,
,
注意到![]() ,
,
从而,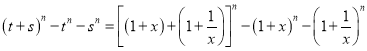
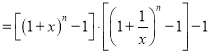
![]()
![]()
![]() ,
,
因此,不等式![]() 对一切均
对一切均![]() 成立.
成立.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目