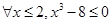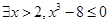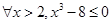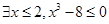题目内容
有下述命题
①若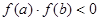 ,则函数
,则函数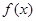 在
在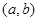 内必有零点;
内必有零点;
②当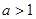 时,总存在
时,总存在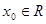 ,当
,当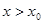 时,总有
时,总有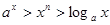 ;
;
③函数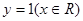 是幂函数;
是幂函数;
④若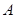

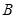 ,则
,则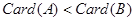 其中真命题的个数是( )
其中真命题的个数是( )
①若
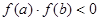 ,则函数
,则函数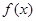 在
在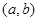 内必有零点;
内必有零点;②当
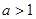 时,总存在
时,总存在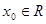 ,当
,当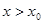 时,总有
时,总有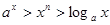 ;
;③函数
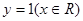 是幂函数;
是幂函数;④若
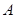

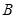 ,则
,则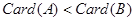 其中真命题的个数是( )
其中真命题的个数是( )| A.0 | B.1 | C.2 | D.3 |
B
试题分析:①若
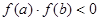 ,则函数
,则函数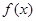 在
在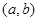 内必有零点,若函数
内必有零点,若函数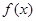 在
在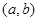 内不连续,就没有零点,故为命题假;②当
内不连续,就没有零点,故为命题假;②当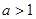 时,总存在
时,总存在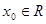 ,当
,当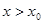 时,总有
时,总有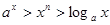 ,在区间
,在区间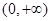 上,尽管指数函数
上,尽管指数函数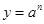 (
(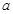 >1),幂函数
>1),幂函数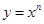 (
(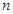 >0),对数函数
>0),对数函数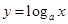 (
(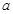 >1)在区间
>1)在区间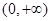 上都是增函数,但它们的增长速度不同,而且不在同一个‘档次’上,随着
上都是增函数,但它们的增长速度不同,而且不在同一个‘档次’上,随着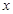 的增大,指数函数
的增大,指数函数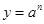 的增长速度越来越快,会超过并远远大于幂函数
的增长速度越来越快,会超过并远远大于幂函数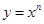 的增长速度,而对数函数
的增长速度,而对数函数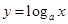 (
(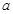 >1)的增长速度则会越来越慢.因此,总会存在一个
>1)的增长速度则会越来越慢.因此,总会存在一个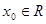 ,当
,当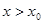 时,就有
时,就有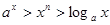 ;故为真命题,③函数
;故为真命题,③函数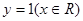 是幂函数,不是幂函数,它是常数函数,故为命题假;④若
是幂函数,不是幂函数,它是常数函数,故为命题假;④若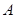

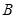 ,则
,则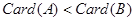 ,当
,当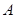 ,
,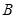 都是无限集时,就不成立,故为命题假.
都是无限集时,就不成立,故为命题假.
练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
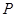 :对任意实数
:对任意实数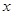 都有
都有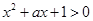 恒成立;
恒成立;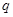 :关于
:关于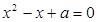 有实数根;如果
有实数根;如果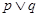 为真,
为真,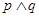 为假,求实数
为假,求实数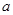 的取值范围.
的取值范围.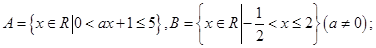
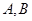 能否相等?若能,求出实数
能否相等?若能,求出实数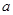 的值,若不能,试说明理由?
的值,若不能,试说明理由?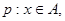 命题
命题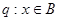 且
且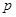 是
是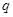 的充分不必要条件,求实数
的充分不必要条件,求实数 有下列命题:①函数
有下列命题:①函数 的图像关于y轴对称;②在区间(-∞,0)上,函数
的图像关于y轴对称;②在区间(-∞,0)上,函数 的最小值为lg2;④在区间(1,+∞)上,函数
的最小值为lg2;④在区间(1,+∞)上,函数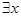 ∈R,
∈R,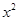 -2ax+a≤0”为假命题,则
-2ax+a≤0”为假命题,则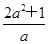 的最小值是__________.
的最小值是__________.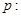 关于
关于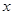 的不等式
的不等式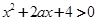 对一切
对一切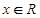 恒成立;命题
恒成立;命题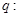 函数
函数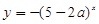 是减函数,若
是减函数,若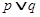 为真命题,
为真命题,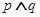 为假命题,则实数
为假命题,则实数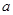 的取值范围为 .
的取值范围为 .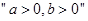 是“方程
是“方程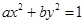 ”表示椭圆的充要条件;
”表示椭圆的充要条件;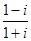 所表示的点在第二象限;
所表示的点在第二象限;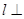 平面
平面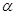 ,平面
,平面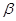 ,则直线
,则直线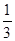 ,则下列复合命题中正确的是( )
,则下列复合命题中正确的是( )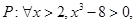 那么
那么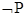 是
是