题目内容
19.已知集合A={x|(|x|-3)(x2+|x|-2)≤0,x∈R},B={x|x2-ax-12≤0,x∈R},若A⊆B,则实数a的取值范围是[-1,1].分析 根据一元二次不等式及绝对值不等式的解法,可先解出集合A={x|-3≤x≤-1,或1≤x≤3},由A⊆B便可知-3,3∈B,从而得到$\left\{\begin{array}{l}{(-3)^{2}-3(-a)-12≤0}\\{{3}^{2}-3a-12≤0}\end{array}\right.$,解该不等式组即可得出实数a的取值范围.
解答 解:x2+|x|-2=(|x|-1)(|x|+2);
由(|x|-3)(x2+|x|-2)≤0得:
$\left\{\begin{array}{l}{|x|-3≥0}\\{{x}^{2}+|x|-2≤0}\end{array}\right.$,或$\left\{\begin{array}{l}{|x|-3≤0}\\{{x}^{2}+|x|-2≥0}\end{array}\right.$;
∴解得1≤|x|≤3;
∴-3≤x≤-1,或1≤x≤3;
∴A={x|-3≤x≤-1,或1≤x≤3};
∵A⊆B;
∴-3∈B,且3∈B;
∴$\left\{\begin{array}{l}{9+3a-12≤0}\\{9-3a-12≤0}\end{array}\right.$;
解得-1≤a≤1;
∴实数a的取值范围为[-1,1].
故答案为:[-1,1].
点评 考查描述法表示集合,高次不等式、一元二次不等式,及绝对值不等式的解法,以及子集的定义元素与集合的关系.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
8.不等式x+2y-1>0表示直线x+2y-1=0( )
| A. | 上方的平面区域 | B. | 下方的平面区域 | ||
| C. | 上方的平面区域(包括直线) | D. | 下方的平面区域(包括直线) |
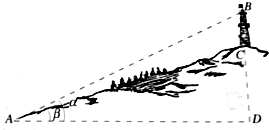 测山上石油钻井的井架BC的高,从山脚A测得AC=65.3m,塔顶B的仰角α是25°25′.已知山坡的倾斜角β是17°38′,求井架的高BC.
测山上石油钻井的井架BC的高,从山脚A测得AC=65.3m,塔顶B的仰角α是25°25′.已知山坡的倾斜角β是17°38′,求井架的高BC.