题目内容
16.已知二次函数f(x)=ax2-2x+a+b(a≠0)的定义域为[0,3],值域为[1,5],求a、b的值.分析 求出f(x)的对称轴为x=$\frac{1}{a}$,讨论a:a<0时,便知f(x)在[0,3]上单调递减,从而值域为[f(3),f(0)]=[1,5],这样可求出a=$\frac{2}{9}$,显然a<0不成立;而a>0时,需讨论$0<\frac{1}{a}<3$,和$\frac{1}{a}≥3$两种情况,在每种情况里根据二次函数f(x)在[0,3]上的单调性或取得顶点情况以及端点的取值情况从而求出a,b,并判断是否符合每种情况的a的范围,从而得出a,b的值.
解答 解:f(x)的对称轴为x=$\frac{1}{a}$;
∴①若a<0,$\frac{1}{a}<0$;
∴f(x)在[0,3]上单调递减;
∴f(x)∈[f(3),f(0)]=[10a+b-6,a+b];
∵f(x)的值域为[1,5];
∴$\left\{\begin{array}{l}{10a+b-6=1}\\{a+b=5}\end{array}\right.$;
解得a=$\frac{2}{9}$,不符合a<0,即这种情况不存在;
②若a>0;
1)若$0<\frac{1}{a}<3$时,$f(\frac{1}{a})=a+b-\frac{1}{a}=1$,而f(0)=a+b=5,或f(3)=10a+b-6=5;
∴解$\left\{\begin{array}{l}{a+b-\frac{1}{a}=1}\\{a+b=5}\end{array}\right.$得,a=$\frac{1}{4}$,$\frac{1}{a}=4$∉(0,3),∴这种情况不存在;
解$\left\{\begin{array}{l}{10a+b-6=5}\\{a+b-\frac{1}{a}=1}\end{array}\right.$得,a=1,或$\frac{1}{9}$,a=$\frac{1}{9}$时,$\frac{1}{a}=9∉(0,3)$;
∴取a=1,b=1;
2)若$\frac{1}{a}≥3$,则f(x)在[0,3]上单调递减;
由①知,a=$\frac{2}{9}$,b=$\frac{43}{9}$,满足$\frac{1}{a}>3$;
∴综上得,a=1,b=1,或$a=\frac{2}{9}$,b=$\frac{43}{9}$.
点评 考查二次函数的对称轴,二次函数的单调性,根据单调性定义求函数值域,或根据二次函数取得顶点情况及端点值的取值情况求二次函数的值域,要熟悉二次函数的图象,求出a之后要判断是否满足讨论的a的取值范围.

| A. | $\frac{3}{2}$ | B. | 9 | C. | $\sqrt{3}$ | D. | 64 |
| A. | A=C且B=D | B. | B=D | C. | A=C | D. | A=B=D |
| A. | AD>$\frac{1}{2}$$\sqrt{2({c}^{2}+{b}^{2})-{a}^{2}}$ | B. | AD=$\frac{1}{2}$$\sqrt{2({c}^{2}+{b}^{2})-{a}^{2}}$ | ||
| C. | AD<$\frac{1}{2}$$\sqrt{2({c}^{2}+{b}^{2})-{a}^{2}}$ | D. | AD≤$\frac{1}{2}$$\sqrt{2({c}^{2}+{b}^{2})-{a}^{2}}$ |
| A. | 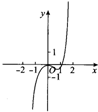 | B. | 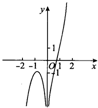 | C. | 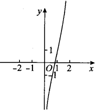 | D. | 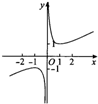 |