题目内容
命题①函数y=f(x)的图象与直线x=a最多有一个交点;
②函数y=-x2+2ax+1在区间(-∞,2]上单调递增,则a∈(-∞,2];
③若
 ,当x∈(0,2)时,f(x)=2x,则
,当x∈(0,2)时,f(x)=2x,则 ;
;④函数y=log2(x2+ax+2)的值域为R,则实数a的取值范围是
 ;
;⑤函数y=f(1+x)与y=f(-x-1)的图象关于y轴对称;
以上命题正确的个数有( )个.
A.2
B.3
C.4
D.5
【答案】分析:根据函数的定义可知,函数y=f(x)的图象与直线x=a的交点时0个或1个;函数y=-x2+2ax+1的对称轴为:直线x=a,开口向下,因为函数在区间(-∞,2]上单调递增,所以a≥2;根据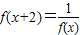 ,可知函数的周期为4,所以f(2011)=f(4×502+3)=f(3)=f(-1),因为
,可知函数的周期为4,所以f(2011)=f(4×502+3)=f(3)=f(-1),因为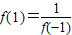 ,f(1)=2,所以f(-1)=
,f(1)=2,所以f(-1)= ;根据函数y=log2(x2+ax+2)的值域为R,可知t=x2+ax+2可取遍一切正数,从而可求实数a的取值范围是
;根据函数y=log2(x2+ax+2)的值域为R,可知t=x2+ax+2可取遍一切正数,从而可求实数a的取值范围是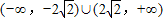 ;函数y=f(1+x)的图象是由函数y=f(x)的图象向左平移一个单位得到,y=f(-x-1)的图象是由y=f(-x)的图象向左平移一个单位得到,而y=f(x)的图象与y=f(-x)的图象关于y轴对称,所以函数y=f(1+x)与y=f(-x-1)的图象关于x=1对称,故可判断.
;函数y=f(1+x)的图象是由函数y=f(x)的图象向左平移一个单位得到,y=f(-x-1)的图象是由y=f(-x)的图象向左平移一个单位得到,而y=f(x)的图象与y=f(-x)的图象关于y轴对称,所以函数y=f(1+x)与y=f(-x-1)的图象关于x=1对称,故可判断.
解答:解:根据函数的定义可知,函数y=f(x)的图象与直线x=a的交点时0个或1个,即最多有一个交点,故①正确;
函数y=-x2+2ax+1的对称轴为:直线x=a,开口向下.因为函数在区间(-∞,2]上单调递增,所以a≥2,故②错误;
∵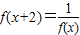 ,∴
,∴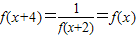 ,∴函数的周期为4,∴f(2011)=f(4×502+3)=f(3)=f(-1),∵
,∴函数的周期为4,∴f(2011)=f(4×502+3)=f(3)=f(-1),∵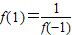 ,当x∈(0,2)时,f(x)=2x,∴f(1)=2,∴f(-1)=
,当x∈(0,2)时,f(x)=2x,∴f(1)=2,∴f(-1)= ,故③正确;
,故③正确;
∵函数y=log2(x2+ax+2)的值域为R,∴t=x2+ax+2可取遍一切正数,∴△=a2-8≥0,∴实数a的取值范围是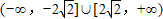 ,故④错误;
,故④错误;
∵函数y=f(1+x)的图象是由函数y=f(x)的图象向左平移一个单位得到,y=f(-x-1)的图象是由y=f(-x)的图象
向左平移一个单位得到,而y=f(x)的图象与y=f(-x)的图象关于y轴对称,所以函数y=f(1+x)与y=f(-x-1)的图象关于x=1对称,故⑤错误
故正确的命题是:①③
故选A.
点评:本题以命题为载体,考查函数的定义,二次函数的单调性,考查函数的值域,考查函数图象的对称性,综合性强,涉及知识点多
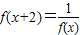 ,可知函数的周期为4,所以f(2011)=f(4×502+3)=f(3)=f(-1),因为
,可知函数的周期为4,所以f(2011)=f(4×502+3)=f(3)=f(-1),因为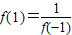 ,f(1)=2,所以f(-1)=
,f(1)=2,所以f(-1)= ;根据函数y=log2(x2+ax+2)的值域为R,可知t=x2+ax+2可取遍一切正数,从而可求实数a的取值范围是
;根据函数y=log2(x2+ax+2)的值域为R,可知t=x2+ax+2可取遍一切正数,从而可求实数a的取值范围是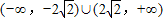 ;函数y=f(1+x)的图象是由函数y=f(x)的图象向左平移一个单位得到,y=f(-x-1)的图象是由y=f(-x)的图象向左平移一个单位得到,而y=f(x)的图象与y=f(-x)的图象关于y轴对称,所以函数y=f(1+x)与y=f(-x-1)的图象关于x=1对称,故可判断.
;函数y=f(1+x)的图象是由函数y=f(x)的图象向左平移一个单位得到,y=f(-x-1)的图象是由y=f(-x)的图象向左平移一个单位得到,而y=f(x)的图象与y=f(-x)的图象关于y轴对称,所以函数y=f(1+x)与y=f(-x-1)的图象关于x=1对称,故可判断.解答:解:根据函数的定义可知,函数y=f(x)的图象与直线x=a的交点时0个或1个,即最多有一个交点,故①正确;
函数y=-x2+2ax+1的对称轴为:直线x=a,开口向下.因为函数在区间(-∞,2]上单调递增,所以a≥2,故②错误;
∵
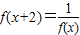 ,∴
,∴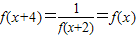 ,∴函数的周期为4,∴f(2011)=f(4×502+3)=f(3)=f(-1),∵
,∴函数的周期为4,∴f(2011)=f(4×502+3)=f(3)=f(-1),∵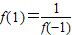 ,当x∈(0,2)时,f(x)=2x,∴f(1)=2,∴f(-1)=
,当x∈(0,2)时,f(x)=2x,∴f(1)=2,∴f(-1)= ,故③正确;
,故③正确;∵函数y=log2(x2+ax+2)的值域为R,∴t=x2+ax+2可取遍一切正数,∴△=a2-8≥0,∴实数a的取值范围是
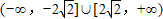 ,故④错误;
,故④错误;∵函数y=f(1+x)的图象是由函数y=f(x)的图象向左平移一个单位得到,y=f(-x-1)的图象是由y=f(-x)的图象
向左平移一个单位得到,而y=f(x)的图象与y=f(-x)的图象关于y轴对称,所以函数y=f(1+x)与y=f(-x-1)的图象关于x=1对称,故⑤错误
故正确的命题是:①③
故选A.
点评:本题以命题为载体,考查函数的定义,二次函数的单调性,考查函数的值域,考查函数图象的对称性,综合性强,涉及知识点多

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目