题目内容
13．设函数f（x）定义在（-1，1）上，求证：f（x）+f（-x）是偶函数，f（x）-f（-x）是奇函数．分析 根据函数奇偶性的定义进行判断即可．
解答 证明：∵f（x）定义在（-1，1）上，
∴由$\left\{\begin{array}{l}{-1＜x＜1}\\{-1＜-x＜1}\end{array}\right.$，即-1＜x＜1，
则设g（x）=f（x）+f（-x），
则g（-x）=f（-x）+f（x）=g（x），则g（x）为偶函数，
设h（x）=f（x）-f（-x），
则h（-x）=f（-x）-f（x）=-[f（x）-f（-x）]=-h（x），则f（x）-f（-x）是奇函数．
点评 本题主要考查函数奇偶性的判断，根据奇偶性的定义是解决本题的关键．
练习册系列答案
相关题目
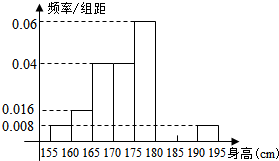从某学校高三年级共800名男生中随机抽取50人测量身高．据测量，被测学生身高全部介于155cm到195cm之间，将测量结果按如下方式分成八组：第一组[155，160）；第二组[160，165）；…；第八组[190，195]．如图是按上述分组方法得到的频率分布直方图的一部分．已知第一组与第八组人数相同，第六组、第七组、第八组人数依次构成等差数列．
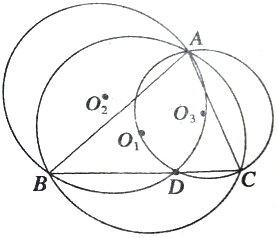如图，D是△ABC的BC边上的一点，O1，O2和O3分别为△ABC，△ADB和△ADC外接圆的圆心，求证：A，O2，O1，O3四点共圆．