题目内容
【题目】如图,以棱长为1的正方体的具有公共顶点的三条棱所在直线为坐标轴,建立空间直角坐标系Oxyz,点P在对角线AB上运动,点Q在棱CD上运动.
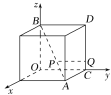
(1)当P是AB的中点,且2|CQ|=|QD|时,求|PQ|的值;
(2)当Q是棱CD的中点时,试求|PQ|的最小值及此时点P的坐标.
【答案】(1)![]() (2) 点P的坐标为(
(2) 点P的坐标为(![]() ), 最小值为
), 最小值为![]() .
.
【解析】
(1)根据正方体的性质可得![]() 的坐标,由两点间的距离公式计算可得结果;(2)根据题意,设点
的坐标,由两点间的距离公式计算可得结果;(2)根据题意,设点![]() 的横坐标为
的横坐标为![]() ,得
,得![]() =
=![]() .由
.由![]() ,可得
,可得![]() =
=![]() =
=![]() ,可得
,可得![]() 的坐标为
的坐标为![]() ,进而可以用
,进而可以用![]() 表示
表示![]() 的长,结合二次函数的性质分析可得结果.
的长,结合二次函数的性质分析可得结果.
(1)因为正方体的棱长为1,P是AB的中点,所以P(![]() ).
).
因为2|CQ|=|QD|,所以|CQ|=![]() ,所以Q(0,1,
,所以Q(0,1,![]() ).
).
由两点间的距离公式得:
|PQ|=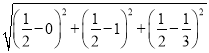 =
=![]() .
.
(2)如图,过点P作PE⊥OA于点E,则PE垂直于坐标平面xOy.
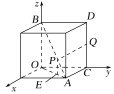
设点P的横坐标为x,则由正方体的性质可得点P的纵坐标也为x.
由正方体的棱长为1,得|AE|=![]() (1-x).
(1-x).
因为![]() ,
,
所以|PE|=![]() =1-x,
=1-x,
所以P(x,x,1-x).
又因为Q(0,1,![]() ),
),
所以|PQ|=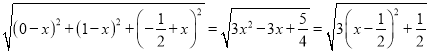
所以当x=![]() 时,|PQ|min=
时,|PQ|min=![]() ,即当点P的坐标为(
,即当点P的坐标为(![]() ),
),
即P为AB的中点时,|PQ|的值最小,最小值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目