题目内容
(本题满分12分)如图,在侧棱垂直于底面的三棱柱 中,
中, 点
点 是
是 的中点.
的中点.

(Ⅰ)求证: ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
(1)证明:见解析;(2)见解析;(3)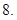
【解析】
试题分析:(1)三棱柱ABC-A1B1C1中,底面三边长AC,BC,AB满足勾股定理则AC⊥BC,又侧棱垂直于底面ABC,则CC1⊥AC,又BC∩CC1=C,根据线面垂直的判定定理可知AC⊥面BCC1,又BC1⊂平面BCC1,根据线面垂直的性质可知AC⊥BC1.
(2)设CB1与C1B的交点为E,连接DE,根据D是AB的中点,E是BC1的中点,可知DE∥AC1,而DE⊂平面CDB1,AC1⊄平面CDB1,根据线面平行的判定定理可知AC1∥平面CDB1;
(3)利用线面垂直得到几何体的高,进而求解体积。
解:(1)证明:在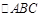 中,
中,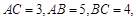
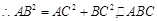 为
为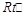 ,
,
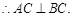 …………………1分
…………………1分
又 底面
底面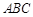 ,
, 底面
底面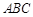 ,
,
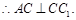 ……………………2分
……………………2分
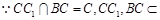 平面
平面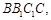
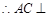 平面
平面 ,……………………………………………………3分
,……………………………………………………3分
而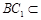 平面
平面 ,
,
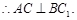 ………………………………………………………………4分
………………………………………………………………4分
(2)设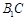 交
交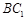 于
于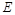 点,连结
点,连结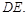
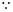 直三棱柱
直三棱柱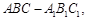
 四边形
四边形 是平行四边形,
是平行四边形, 是
是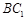 的中点……………………………5分
的中点……………………………5分
又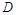 是
是 的中点,
的中点,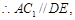 ………………………………………………6分
………………………………………………6分
而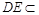 平面
平面 ,
,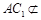 平面
平面 ,………………………………………7分
,………………………………………7分
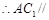 平面
平面 .………………………………………………8分
.………………………………………………8分
(3)连结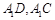 ,过点
,过点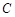 作
作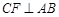 ,垂足为
,垂足为 .
.
在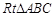 中,
中,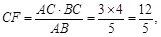 ………………………………9分
………………………………9分
又 直三棱柱
直三棱柱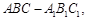
 平面
平面 平面
平面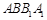 ,而
,而
平面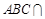 平面
平面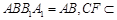 平面
平面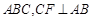
 平面
平面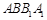 ,即
,即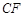 是三棱锥
是三棱锥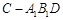 的高,…………………………11分
的高,…………………………11分
又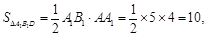 ………………………………………12分
………………………………………12分
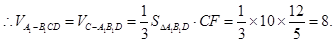
考点:本试题主要考查了空间几何体中线线垂直的证明,以及线面平行判定定理的熟练运用。
点评:解决该试题的关键是根据线面垂直的判定定理得到线线垂直,以及运用线面平行判定定理证明线面平行。同时结合前两问的结论,作出几何体的高。

 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
