题目内容
(2013•湖南模拟)下列命题中正确的命题个数为( )
①存在一个实数x使不等式
-3x+6<0成立;
②已知a,b是实数,若ab=0,则a=0且b=0;
③x=2kπ+
(k∈Z)是tanx=1的充要条件.
①存在一个实数x使不等式
| x | 2 |
②已知a,b是实数,若ab=0,则a=0且b=0;
③x=2kπ+
| π |
| 4 |
分析:对于①,由于
-3x+6的△<0,从而
-3x+6>0恒成立,据此对①进行判断;②若ab=0,则a=0或b=0;从而进行判断;③当x=2kπ+
(k∈Z)时,得出 tan(2kπ+
)=tan
=1,“x=2kπ+
(k∈Z)”是“tanx=1”成立的充分条件;举反例x=
时,tan
=1.推出“x=2kπ+
(k∈Z)”是“tanx=1”成立的不必要条件,据此进行判断.
| x | 2 |
| x | 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
| 5π |
| 4 |
| π |
| 4 |
解答:解:
-3x+6的△=9-26<0,∴
-3x+6>0恒成立,
故①不正确;
对于②若ab=0,则a=0或b=0,故②不正确;
③tan(2kπ+
)=tan
=1,所以充分;但反之不成立,如 tan
=1.
故x=2kπ+
(k∈Z)是tanx=1的充分不必要条件.故③不正确.
∴命题中正确的命题个数为0.
故选A.
| x | 2 |
| x | 2 |
故①不正确;
对于②若ab=0,则a=0或b=0,故②不正确;
③tan(2kπ+
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
故x=2kπ+
| π |
| 4 |
∴命题中正确的命题个数为0.
故选A.
点评:本题主要考查了命题的真假判断与应用,必要条件、充分条件与充要条件的判断.充分条件与必要条件是中学数学最重要的数学概念之一,要理解好其中的概念.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 (2013•湖南模拟)设椭圆
(2013•湖南模拟)设椭圆 (2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
(2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=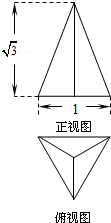 (2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
(2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( ) (2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )
(2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )